Uforandret opbygning af træet	Når man ønsker at bevare et træ balanceret er AVL-træer en rimelig enkel løsning. Fordelen ved AVL-træer frem for andre teknikker er, at det binære søgetræes strukturelle opbygning er uforandret. AVL står for Adelson-Velsky og Landis, der er ophavsmænd til disse træer.
AVL-betingelsen	Definition: AVL-træ Et AVL-træ er et binært søgetræ, hvor der for hver knude gælder, at højdeforskellen mellem dets to undertræer højest er 1.
Rimelig balanceret	Definitionen er ikke streng nok til at garantere et fuldt træ. Det betyder dog, at træet er rimelig balanceret, så man stadig kan opnå logaritmiske tidskompleksiteter.
Logaritmisk højde	Man kan vise, at AVL-træer har logaritmisk højde, idet antallet af knuder i et AVL-træ med højde h er mindst det h+2'te fibonacci-tal. Det bemærkes at fibonacci-tallene vokser exponentielt, hvorfor højden bliver logaritmisk.
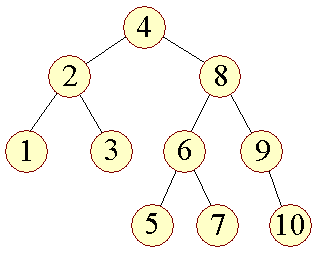
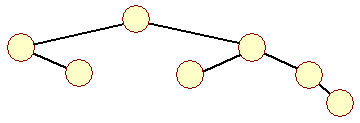
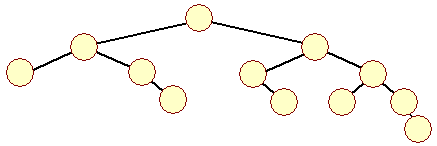
	En af de processer der normalt kan ødelægge et binært træes balancering er indsættelse af en sorteret sekvens af data. Det vil udarte sig til en vestjysk palme som illustreret i kapitlet om balancerede træer. Når vi arbejder med AVL-træer, skal vi naturligvis ændre vores algoritmer til indsættelse, sletning osv., så de bibeholder træet som et AVL-træ efter terminering. Et AVL-træ vil efter indsættelse af talrækken 1, 2, ... , 10, få følgende udseende:
Figur 1: AVL træ efter indsættelse af ordnet talrække
	1. Indsættelse
	Ved indsættelse placerer man elementet som ved normal indsættelse i binære søgetræer. Dernæst genopretter man, om nødvendigt, AVL-betingelsen.
	Vi vil i den forbindelse indføre et begreb, der hedder pivotknuden:
Pivotknuden	Definition: Pivotknuden Pivotknuden er den knude længst nede på søgestien, til det netop indsatte element, der var ude af balance før indsættelse.
Passerer pivotknuden	Da vi ved indsættelse i et binært søgetræ reelt søger efter elementet, vil vi passere pivotknuden, og vil derfor efter den almindelige indsættelse kende pivotknuden. Det interessante ved pivotknuden er, at vi ved ødelagt AVL-betingelse kun behøver at ændre fra pivotknuden og nedad, for at genoprette AVL-betingelsen. Man får ikke brug for at gå langt ned i træet, men kan nøjes med at arbejde med pivotknudens børn og børnebørn.
	Lad os studere nogle eksempler på, hvordan situationen kan ændre sig ved almindelig indsættelse.
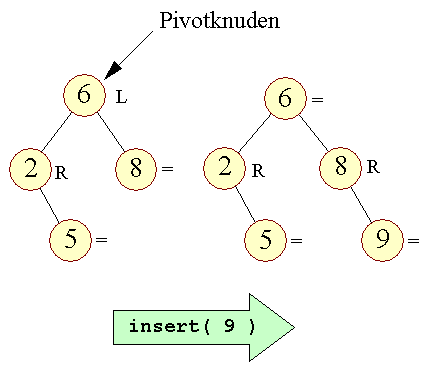
Figur 2: Pivotknude og indsættelse
Venstre- og højre-tung	I figuren betyder et L ved en knude, at den er venstre-tung. Dvs. at dens venstre undertræ er én højere end dens højre. Tilsvarende betyder R at den er højre-tung og = at undertræerne er lige høje.
Ingen problemer i pivotknudens laveste undertræ	Da vi her indsætter i pivotknudens højre undertræ, kan vi blot justere mærkerne på søgestien. Da alle knuder på søgestien under pivotknuden før indsættelse er balancerede, kan indsættelsen højest ændre disse mærker med én! Derfor har knuder på søgestien under pivotknuden aldrig problemer. Hvis der skal indsættes en knude i pivotknudens laveste undertræ kan pivotknuden heller ikke få problemer, da den kan tåle at blive ændret hele to mod den side der indsættes i. Det er netop tilfældet i vores eksempel, hvor 9 indsættes i 6's laveste undertræ.
	I de situationer, hvor pivotknuden kan tåle indsættelse af det nye element uden at sprænge rammerne for AVL-betingelsen, kan man nøjes med at justere mærkerne på søgestien.
	Ud fra vores ræsonnement ovenfor har vi isoleret problemerne til kun at kunne opstå i den situation, hvor der indsættes i pivotknudens højeste undertræ.
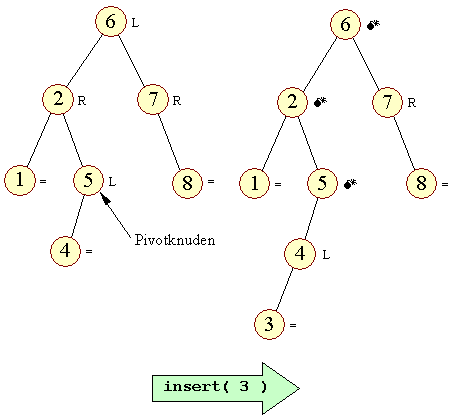
Figur 3: Sprængning af AVL-betingelsen
Sprængning af AVL-betingelsen	Her har vi problemet. Pivotknudens rammer for ubalancerethed sprænges mht. AVL-betingelsen. En sprængning der spreder sig op i søgestien fra pivotknuden. Vi er derfor nød til at flytte knuder:
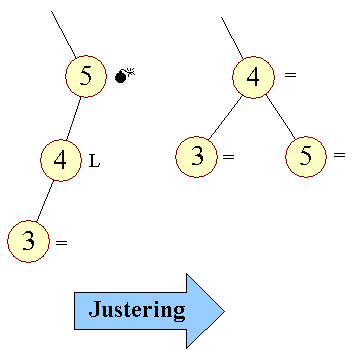
Figur 4: Efterjustering
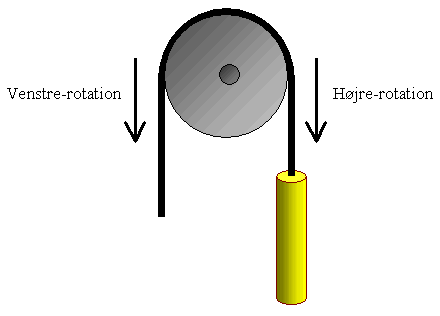
Rotation	Det der sker her, kaldes en højrerotation. Navnet rotation beskriver den bevægelse de tre knuder som kæde har udført.
	Man kan illustrere det med et gammeldags stue-ur. Urværket bliver trukket af et lod, der bevæger et tandhjul. Når man skal trække uret op, gør man det ved at trække i den modsatte side af loddet. I forbindelse med rotationer ønsker vi enten at trække den ene eller den anden vej, så vi enten får løftet eller sænket knuder i træet.
Figur 5: Gammeldags stue-ur
	Når vi skal beskrive de situationer, hvor justeringer er nødvendige, vil vi anvende forkortelser for de implicerede knuder: P: pivotknuden, F: faderen til pivotknuden, B: pivotknudens barn på søgestien, BB: pivotknudens barnebarn på søgestien og E: den indsatte knude.
	Vi kan inddele de situationer, hvor vi skal foretage justeringer af knuder, i to grupper.
	1. E indsættes i B's højre undertræ, og B er roden i P's højre undertræ, som samtidig er P's højeste undertræ (tilsvarende kunne det være venstre-venstre)
Figur 6: Indsættelse i P's højre-højre undertræ
Skal bevare ordningen i søgetræet	Balancerne er i figuren vist før indsættelsen. Det er for de tre undertræer angivet, med fortløbende numre, hvilken ordning de repræsenterer. Når vi ændrer, må vi derfor ikke bytte om på rækkefølgen læst fra venstre mod højre, da vi ellers vil bryder ordningen i søgetræet.
	Det venstre undertræ skal skubbes ned og det højre skubbes op. Det midterste skal enten løftes eller bevares i dets niværende niveau.
Venstre-rotation	Vi laver derfor en venstre-rotation ved at løfte B op på P's plads og skubbe P ned som venstre barn til B. Samtidig lader vi det midterste træ blive højre undertræ for P, så B får plads til P, som venstre barn. Resultatet bliver:
Figur 7: Efter venstre rotation
Spejlvendte situation	Den spejlvendte situation, hvor E indsættes i B's venstre undertræ, og B er roden i P's venstre undertræ, som samtidig er P's højeste undertræ, laves tilsvarende med en højre-rotation.
	2 Det er ikke venstre-venstre eller højre-højre i P's højeste undertræ, men venstre-højre eller højre-venstre.
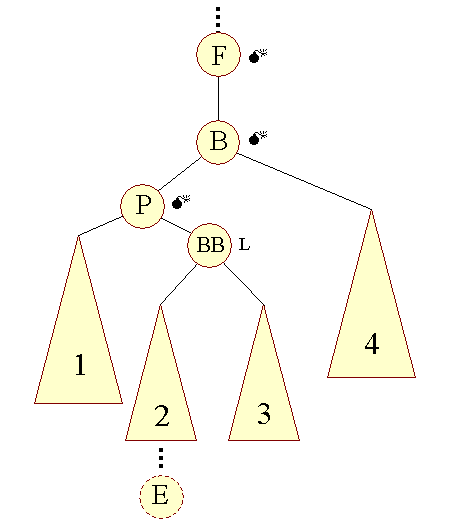
	Lad os se konkret på problematikken med højre-venstre undertræ:
Figur 8: Almindelig indsættelse i højre-venstre undertræ
	Vi har også her anført P's barnebarn BB og dermed i figuren foretaget et valg mht. i hvilket af BB's undertræer E indsættes i. Som vi vil se i det følgende er det uden betydning for algoritmen, om E er indsat i det ene eller det andet.
	Det vil være besnærende at lave en venstre-rotation omkring P for at hive op i P's højre undertræ, som det er gjort i følgende firgur. Men som man ser vil det kun have effekt på den yderste del (her den højre) af P's højeste undertræ (her det højre undertræ).
Figur 9: Venstre-rotation uden ønsket effekt
	Vi skal derfor først ændre balancen i højre undertræ til P, så et træk opad i højre side vil virke!
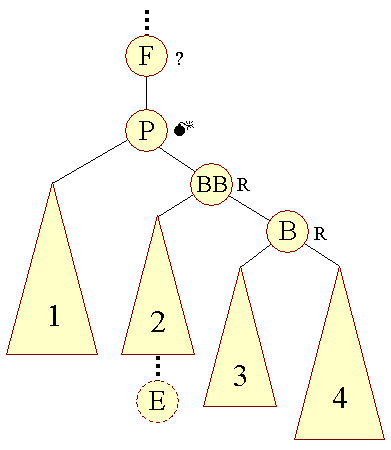
	Hvis vi ser pivot-agtigt på B, kan vi ændre balancen omkring B ved en enkelt højrerotation:
Figur 10: Efter forberedende højre-rotation om B
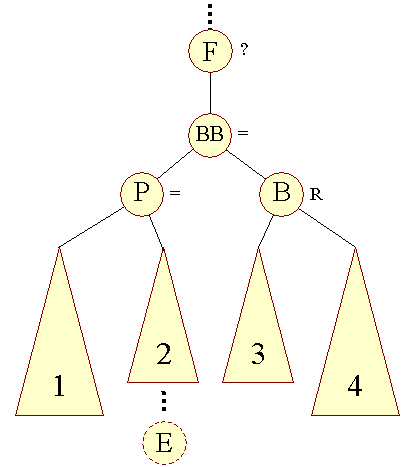
	Efter vi nu har rykket op i BB's undertræ er vi klar til den venstre-rotation om P vi før forsøgte:
Figur 11: AVL-betingelsen genoprettet efter venstre-rotation
	Vi ser her, som lovet, at algoritmen ikke er afhængig af om E er indsat i undertræ 2 eller 3!
	Situationen med venstre-højre løses analogt.
Dobbelt-rotation	Da man laver to på hinanden følgende rotationer, kalder man det dobbelt-rotation. Man kalder det mere præcist en dobbelt højre-rotation, når den første er en enkelt højre-rotation og visa versa.
	2. Sletning
	[mangler - fungerer analogt, men efter sigende lidt mere kompliceret - det må vente til senere]
	3. Implementering
	For at kunne foretage justeringer må vi tilknytte en ekstra information til hver knude. Det, vi vil registrere er, om de to undertræer er balancerede eller, om venstre eller højre undertræ er højest. Vi udvider vores almindelige Node klasse med en integer variabel balance til dette formål, og laver et interface Balance til at definere balanceringerne som tre konstanter:
Source 1: knude med balance	interface Balance { public static final int LEFT = 0; public static final int EVEN = 1; public static final int RIGHT = 2; } class Node { public Node left, right; public int balance; }
	[mangler resten - må vente til senere]
	Repetitionsspørgsmål
1	Hvad er fordelen ved AVL-træer frem for andre balanceringsteknikker?
2	Hvad er AVL-betingelsen?
3	Er et AVL-træ et fuldt træ?
4	Hvad er pivotknuden?
5	Når man skal genoprette AVL-betingelsen; hvilke knuder er det så nødvendigt at arbejde med?
6	Hvad vil det sige at en knude er henholdsvis højre- eller venstre-tung?
7	Hvornår er der aldrig behov for at flytte knuder for at genoprette AVL-betingelsen?
8	Hvordan er situationen hvis pivotknudens undertræer er lige høje?
9	Hvorfor kalder man de knudeflytninger vi laver for rotationer?
10	Er en dobbelt venstre-rotation en højre-rotation efterfulgt af en venstre-rotation eller omvendt?
	Projekter
1	Lad os se hvor skævt et AVL-træ det er muligt at konstruere. Vi vil prøve at lave det så højreskævt som muligt. Fremgangsmåden er for hvert skridt at føje et blad på yderst til højre og sætte blade på andre steder (så højrestillede som muligt) for at retablere AVL-betingelsen.
	I første skridt får vi:
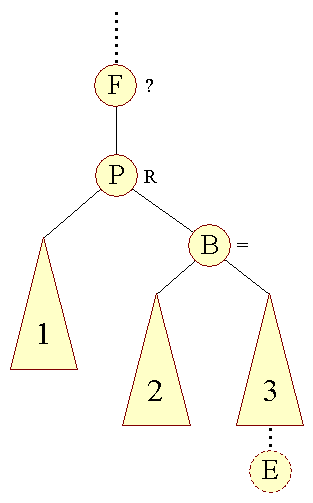
	I andet skridt:
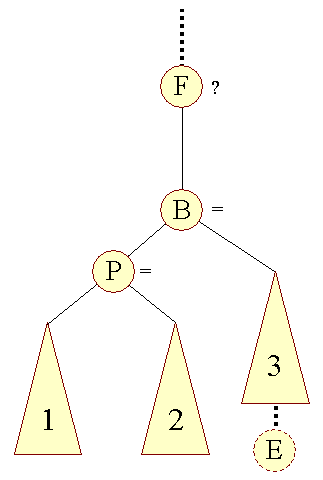
	I tredie skridt:
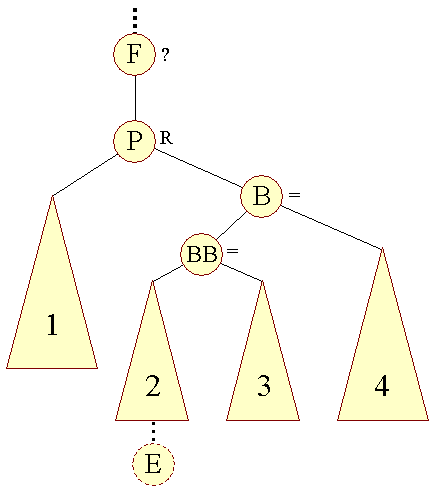
	I fjerde skridt:
Fraktal	Et maksimalt højreskævt AVL-træ er en fraktal [FKJ]. Der fremkommer ved hjælp af følgende starttilstand:
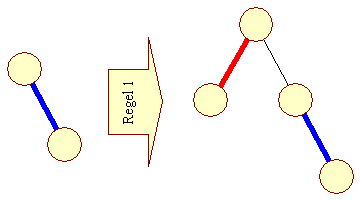
	Der er to regler der styrer udviklingen, i hver iteration. Den først gælder for ethvert højre-blad:
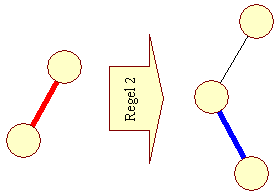
	Mens den næste gælder for ethvert venstre-blad:
	Lav et program der tegner denne fraktal. F.eks. i en Canvas
	Svar på repetitionsspørgsmål
1	At træstrukturen stadig er et almindeligt binært søgetræ.
2	At højdeforskellen mellem to undertræer for enhver knude er højest én.
3	Det kan det være, men det er på ingen måde sikkert.
4	Det er den knude længst nede af søgestien der er ude af balance før indsættelse.
5	Det er højest nødvendigt at arbejde med pivotknudens dens barn og barnebarn på søgestien ned mod stedet hvor der er indsat en ny knude.
6	At henholdsvis det højre eller venstre undertræ er én højere end det andet.
7	Når der indsættes i pivotknudens laveste undertræ.
8	Trick-spørgsmål: Hvis pivotknudens undertræer har samme højde, er den ikke en pivotknude.
9	Fordi de visuelt ligner rotationer af "knude-kæder" omkring en knude.
10	Det er omvendt.