| Arrays giver hurtig adgang til elementerne |
Arrays har en fordel frem for andre datastrukturer — tilgangen til elementerne er meget hurtig. Vil man have et bestemt element, kan man med dets index foretage et opslag med konstant tidskompleksistet: O(1).Det er dog ikke i alle situationer det er hensigtsmæssigt at bruge et array. For det første er størrelsen af et array statisk, men der er også spørgsmålet om spredning af index. Det er det sidste vil vi beskæftige os med i dette kapitel. |
| |
0.1 Spredning af nøgle-værdier/index |
| |
Man vælger normalt index for et element, som en slags nøgle, men hvad hvis der er stor spredning på disse nøgler. |
| CPR-numrer |
Tag f.eks. et CPR-register. Et CPR-nummer ligger groft sagt i intervallet fra 100.000.000 til 3.100.000.000. I dette interval er langt de fleste tal ikke CPR-numrer, og fra 0 op til 100.000.000 er der slet ingen! Vil vi derfor bruge et (stort) array til at opbevare CPR-oplysninger, skal vi have et array med ca. 3.1 millarder indgange; hvoraf vi kun bruger en meget lille del af dem. Hullet op til 100.000.000 kan fjernes ved at trække dette tal fra, henholdsvis lægge det til, når vi tilgår array'et, men vi vil stadig have et meget "tyndt" besat array! |
| |
1. Hash-funktioner |
| Afbilde nøgler over i index |
Løsningen kunne være at afbilde nøglerne over i index med en funktion. Når vi direkte anvender nøglerne som index, bruger vi på sin vis identitets-funktionen: f(x) = x. Skal vi have fjernet hullerne i arrayet, og dermed kunne nøjes med et mindre, må funktionen skulle afbilde nøgle-rummet ind i et index-rum, med en lavere kardinalitet (mængde med færre elementer). En sådan funktion kunne f.eks. være: |
|
|
| |
Denne funktion ville afbilde over i en mængde med 1.000 elementer, dvs. 1.000 index! Vi kan nu nøjes med et array med 1.000 indgange. |
| Kollisioner |
En sådan funktion kaldes en hash-funktion og der findes mange af slagsen. Fælles for dem alle er at de løser ét problem og giver os et nyt. De løser problemet med det store index-rum, men til gengæld vil de afbilde forskellige nøgler over i det samme index — vi vil få kollisioner! |
| |
1.1 Kvaliteter |
| |
Når vi skal finde en god hash-funktion, vurderer vi dem efter en række kvaliteter. |
|
- Funktionen skal være hurtig at beregne
- Afbildningen skal sprede index jævnt ud over array'et
|
| Hurtig |
Hash-funktionen skal ikke ødelægge den hurtige adgang vi har med et array. Det er derfor vigtigt at den ikke sinker tilgangen mere en højest nødvendigt. Vi vil derfor gerne have en simpel, og dermed hurtigt funktion. |
| Jævn spredning |
Afbildningen skal give en jævn fordeling, så værdierne ikke klumper sammen i array'et. Det har specielt betydning, når vi senere skal se, hvordan vi håndterer kollisioner. |
| |
1.2 Typer |
| |
Når man laver en hash-funktion konstruerer man den normalt ud fra en af følgende principper. |
| |
1.2.1 Almindelig afrunding |
| |
Ved Afrunding (eng.: truncation) ser vi bort fra en del af nøglen. F.eks. kunne vi i eksemplet med CPR-numre vælge at se bort fra løbenummeret, og bruge et array me 1.000.000 indgange. I det konkrete eksempel vil det ikke give en jævn spredning over index-mængden, da der vil blive mange huller — f.eks. vil ingen af nøglen blive afbildet ind i de index på formen: xx32xx til xx99xx, da måneden altid vil ligge mellem 1 og 31. Hash-funktionen vil være: |
|
|
| |
med heltalsdivision. Det er en hurtig funktion, men den kræver at cifrene der bliver tilbage er jævnt fordelt; hvilket f.eks. ikke er tilfældet for CPR-numre. |
| |
Som nævnt betyder afrunding ikke blot være en heltals-afrunding, det kan være en hvilken som helst funktioner, der klipper en del af nøglen, der kan anvendes som index. Den kan derfor også basere sig på modulus. |
| |
1.2.2 Modulus-baseret afrunding |
| |
Vælger man at basere den på modulus, bruger man array'ets størrelse: |
|
|
| |
Funktionen er meget bekvem, idet den indstiller sig efter array'ets størrelse og ikke omvendt. Det omvendte er netop tilfældet ved almindelig afrunding, som er beskrevet ovenfor. |
| |
Igen en hurtig funktion, men igen skal man være opmærksom på hvor jævn en fordeling den giver. Er nøgle-mængden i sig selv jævnt fordelt, er en modulus-baseret hash-funktion normalt en glimrende funktion at anvende. |
| |
1.2.3 Foldning |
| |
Ved foldning skærer man nøglen i mindre stykker og "lægger dem sammen", typisk ved simpel addition, efterfuldt af en afrunding. Hvis vi f.eks. vil afbilde telefon-numre over i index, kan vi opdele de 8 cifre i fire grupper af 2, lægge disse fire tal sammen og tage modulus 100. F.eks.: |
|
f( 96606500 ) = ( 96 + 60 + 65 + 00 ) % 100 = 221 % 100 = 21
|
| |
Fordelen ved foldning er at den i modsætning til afrunding ikke er afhængig af en jævn fordeling i dele af nøglen. Den "folder" flere dele af nøglen sammen, så deres individuelle spredning bliver "rodet sammen". En lille ulempe ved foldning, er at den er en anelse langsomere end afrunding. |
| |
2. Håndtering af kollisioner |
| |
Uanset hvilken hash-funktion vi vælger, vil vi stå med kollisions-problemet: der er flere nøgler der afbildes over i det samme index. I den forbindelse er der en faktor som vi bruger til at beskrive hvor fyldt et array er: |
| Load factor |
Definition: Load factor
Load factor'en er lig med forholdet mellem antallet af elementer i array'et og index-mængdens størrelse.
L = #elementer / #indgange
L vil altid ligge i intervallet: [0:1]
|
| |
Der findes i hovedsagen to måder at håndtere dette problem: åben adressering og chaining. |
| |
2.1 Åben adressering |
| Finde et andet sted |
I åben adressering er resonnementet som så: hvis der allerede er et element i den pågældende indgang af array'et, så må vi finde et andet sted. Dette kan "andet sted" kan vælges på mange måder, og vi vil her indskrænke os til to af de mest kendte: lineær og kvadratisk probing: |
| |
2.1.1 Lineær probing |
| |
Ved lineær probing er idéen at se på den næste indgang, og om nødvendigt den næste igen, indtil vi finder en ledig plads. Lad os se et eksempel: |
Figur 1:
Kollision |
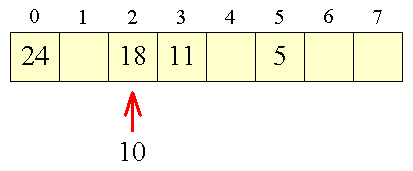 |
| |
Vi anvender her den modulus-baserede hash-funktion: |
|
|
| |
Vi får en kollision, da 10's plads allerede er optaget. Ved lineær probing bliver 10 derfor placeret i indgang 4: |
Figur 2:
Lineær probing |
 |
| |
Når efterfølgende søger efter f.eks. 10 gør vi det samme - vi beregner hash-funktionen af 10, og starter med at søge lineært fra det beregnede index og fremefter, til vi enten finder det søgte element eller en tom indgang. |
| |
Lineær probing har et problem, som man allerede fornemmer af overstående eksempel - det klumper sammen! Problemet med disse klumper er, at man ved søgning kommer til at skulle lave liniær søgning i større eller mindre omfang. Jo større klumper, jo mere lineær søgning! |
| |
For at undgå disse klumper har man forsøgt at modificere lineær probing, ved at lave spring fremad i array'et - f.eks. ved kvadratisk probing: |
| |
2.1.2 Kvadratisk probing |
| |
Når der er en kollision på en indgang i, vil man i kvadratisk probing dernæst prøve i indgang: i+12, i+22, i+32, ... - dvs. i+x2, hvor x = 1, 2, 3, .... Mao.: i+1, i+4, i+9, .... Når værdierne bliver for store for index-mængden, "bøjes de rundet" med modulus. |
| |
Kvadratisk probing opnår på denne måde er større spredning ved kollision, men der opstår et andet problem: Vi udnytter ikke hele array'et! |
| |
Umiddelbart skulle man tro nøglerne ville blive afbildet ind i index-mængden, i noget der lignede en tilfælde "regn" af tal, men det gør de ikke. Det viser sig at man, selv med et array med en længde der er et primtal, kun vil ramme halvdelen af indgangene [Rowe97]. Det betyder dog at kvadratisk probing er udemærket så længde load-faktoren holder sig under 0.5 [Weiss01]. |
| |
2.1.3 Problemer med sletning |
| |
Åben adressering er rimelig ukompliceret, men har et stort problem: Det er meget vanskeligt at slette allerede indsatte elementer. |
| |
Problemet ligger i, at elementernes placering er afhængige af de andre elementer. Når et element indsættes vil dets placering ikke alene blive afgjort af hash-funktionen, men også af den probing der foretages i den aktuelle situation. Fjernes der elementer i array'et vil det bryde denne sammenhæng, og nogle elementer vil ikke længere kunne findes ved at bruge hash-funktionen med tilhørende probing. |
| |
Hvis vi i eksemplet ovenfor ønsker at slette 11: |
Figur 3:
Problem med sletning |
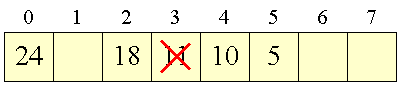 |
| |
får vi et problem med 10. 10 blev indsat i indgang 4 netop fordi indgang 2 og 3 var optaget — en forudsætning der ikke længere holder. Søger vi nu efter 10 vil vi ikke komme længere end til indgang 2, da vi vil tro at den tomme i indgang 3 udlukker, at der kan være flere elementer med en hash-værdi på 2. |
| Lazy deletion |
I praksis skal der laves så meget benarbejde for at retablere en tilstand i array'et der er i overensstemmelse med hash-funktion og den valgte probing, at man ganske enkelt lader være! I stedet vælger man at markere elementer man ønsker slettet, som slettet — man kalder dette: lazy deletion. Derved forbliver elementet på sin plads og man kan bruge det som en dummy, der bevarer sammenhængen, men ellers er "borte". |
| |
2.2 Chaining |
| |
Idéen i chaining er en ganske anden end ved probing. Med chaining finder vi ikke en alternativ indgang ved kollisioner — vi "stabler" dem i stedet! Det gøres i praksis med en hægtet liste, og vores array bliver derfor ikke et array af elementer, men et array, hvor hver indgang har en hægtet liste. |
| |
Vi får nu ikke problemer med sletning, da der ikke opstår huller, og indsættelse får vi tidskompleksiteten O(1), da indsættelse i array'et er ensbetydende med indsættelse i en hægtet liste. Til gengæld kan søgning igen udarte sig til en kortere eller længere lineær søgning. |
| |
Litteratur |
| |
[Rowe97]: "An Introduction to Data Structures and Algorithms with Java", Glenn W. Rowe, Prentice Hall, 1997 |
| |
[Weiss01]: "Data Structures & Problem Solving using Java, 2nd.ed.", Mark Allen Weiss, Addison-Wesley, 2001 |


