Heap betyder dynge	Heaps (eng. heap: dynge, hob ) er binære træer, der er organiseret på en anden måde end binære søgetræer. Binære søgetræer er kendetegnet ved den betingelse, der er knyttet til hver knude i træet: At alle knuder i venstre undertræ er mindre end, og alle knuder i højre undertræ er større end, knuden selv. I heaps er der også pålagt hver knude en ordningsbetingelse, den er dog simplere:
	Definition: Heap-betingelsen For enhver knude gælder der, at begge børn er mindre end eller lig med knuden selv
	I modsætning til det binære søgetræes vandrette ordning er heaps ordnet lodret langs enhver sti.
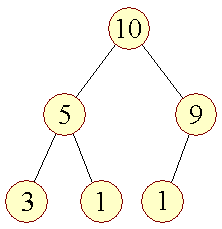
	Lad os se et eksempel på en heap:
Figur 1: Et heap-træ
Justere efterfølgende	I en heap skal vi naturligvis kunne indsætte og udtage elementer. Alle operationer på heaps udføres ved at foretage ændringen uden hensyntagen til heapbetingelsen og dernæst justere, så ordningen bliver genoprettet.
	1. Repræsenteret som array
Repræsenteret som array	Selv om man altid tænker på en heap som et træ, vælger man ofte at repræsentere dette træ som et array! Grunden er, at man kan gøre det på en måde så det er let at komme fra et børn til en fader. Når man arbejder med heaps har man nemlig brug for både at arbejde oppefra/ned og nedefra/op. Det sidste er vanskeligt i en traditionel træ-repræsentation. Man bemærker, at array-repræsentationen har en kedelig konsekvens: En træ-repræsentation med pointere er dynamisk, mens et array er statisk. Det er dog en pris man er villig til at betale, da en array-repræsentation ligeledes gør det nemt at holde træet komplet med deraf følgende logaritmisk højde.
	Vi vil derfor realisere en heap som flg. container-klasse:
Source 1: Container klassen	class Heap { private int nodes[]; private int size; public Heap( int maxNodes ) { nodes = new int[ maxNodes+1 ]; size = 0; } ... }
	Hvor nodes[] er det array der indeholder knuderne og size er det aktuelle antal knuder i arrayet
Level-order	Vi vil lave array-repræsentationen ved at liste knuderne som man læser dem, fra venstre mod højre, og oppefra og ned, også kaldet level-order. Eksemplet fra før, bliver derved:
	nodes: 10 5 9 3 1 1
	Hvis man betragter array-repræsentationen observerer man den sammehæng, at en knude på position i, har sine børn på position 2*i og 2*i+1. Og omvendt, at en knude har sin fader på position i/2. Dette forudsætter dog, at man regner den første position (roden) som 1. Vi vil derfor set bort fra nodes[0], der ikke anvendes i det følgende.
	1.1 Konstruktion
Fra array uden ordning	Vi vil nu studere en algoritme til konstruktion af en heap ud fra et array uden ordning. nodes[] vil altid kunne tolkes som en array-repræsentation af et komplet træ, vi skal blot flytte rundt på knuderne i array'et så det bliver en heap.
	Når man skal konstruere denne array-repræsentation gøres det vha. flg. rekursive metode [AHU 74, s. 90]:
Pseudo 1: Heap-kontruktion	private void heapify( int i, int j ) { if ( "i ikke er et blad" && "$ k: k er barn af i, og A[k]>A[i]" ) { Lad k være den største af i's børn; swap A[i] og A[k]; Heapify( k, j ); } }
Skov af heaps	i og j fortæller metoden hvilket interval af nodes[], der allerede "er" en heap, nemlig ]i:j]. Metoden løser problemet med at føje i til, så [i:j] "bliver" en heap. "er" og "bliver" er sat i anførselstegn, da det at en del af array'et betegnes som en heap, skal forstås på den måde at alle knuder i del-array'et opfylder heapbetingelsen. Det betyder ikke at delarray'et ophøjet til array, med sine deraf følgende nye index, vil være en heap. Heapbetingelsen er kun opfyldt med index-positionerne fra hele array'et. Derfor bør man i stedet se på den del af array'et, der "er" en heap, som en skov af træer, der hver for sig er rigtige heaps.
	Lad os se hvad der sker i træ-repræsentationen
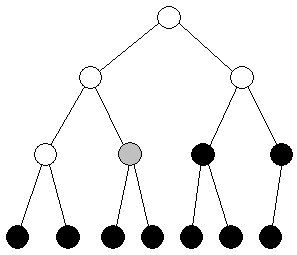
	Situationen kunne på et tidspunkt være flg.:
Figur 2: Skov af heaps
	De sorte knuder er den del ]i:j], der "er" en heap. Den grå knude er den i'te knude som vi nu vil føje til.
	Hvis den grå knude er større end begge sine børn, opfylder den heap-betingelsen og kan den blot gøres sort.
	Hvis en eller flere af børnene er større, vil det største barn være det største af de tre. Vi kan derfor ved at swappe den grå knude med det største barn, skabe en situation, hvor heapbetingelsen er opfyldt, for den position i træet den grå knude var på.
Boble ned	Vi gentager nu denne proces, med at boble den grå knude ned igennem træet, indtil den er større end begge sine børn.
	Da heapify bobler den næste knude ned på plads kunne man kalde den bobleDown, men vi vil forbeholde dette navn til den tilsvarende metode med kun én parameter, hvor j altid er size.
	j kan bruges til at afgøre om i er et blad: Hvis i>j/2 så er i et blad. Hvis i ikke var et blad, skulle den have børn på position 2*i og evt. 2*i+1, men da i>j/2 Þ 2*i>j eksisterer disse positioner ikke (der er igen knuder så langt henne i array'et).
	At undersøge om $ k, hvor k er et barn til knuden på position i, så nodes[k]>nodes[i], altså, at knude i ikke er større end begge sine børn, gøres ved at se på nodes[2*i] og nodes[2*i+1], med indledende check af, at den sidste eksisterer (den første vil altid eksisterer, da i ellers var et blad; hvilket vi startede med at udelukke).
	heapify kan derfor implementeres ved:
Source 2: Heap-kontruktion	private void heapify( int i, int j ) { int t, k; if ( i<=j/2 && ( nodes[2*i]>nodes[i] || 2*i<j && nodes[2*i+1]>nodes[i] ) ) { // find største barn if ( 2*i>=j ) // ikke noget højre barn => venstre er størst k = 2*i; else if ( nodes[2*i] > nodes[2*i+1] ) k = 2*i; else k = 2*i+1; // swap fader og største barn t = nodes[i]; nodes[i] = nodes[k]; nodes[k] = t; heapify( k, j ); } }
	Ikke alene kalder heapify sig selv rekursivt, men den kaldes også talrige gange af den overordnede metode:
Source 3: Den overordnede metode	private void arrayToHeap() { for ( int i=size; i>=1; i-- ) heapify( i, size ); }
Optimering	Man kan i stedet starte ved i=size/2. At dette er muligt kan man se ud fra et argumentet mht. antallet af blade i forhold til knuder i et komplet træ. Hver gang vi fjerner to blade i bunden, bliver der netop ét blad mere i næst-nederste række! Ergo vil halvdelen af alle knuder i et komplet træ være blade.
	At algoritmen virker kan vises ved et baglæns induktionsbevis for:
	Sætning. Hvis knuderne i+1, i+2, ... , size alle opfylder heapbetingelsen, i forhold til deres børn, så vil i, i+1, ... , size ligeledes opfylde heapbetingelsen efter et kald af heapify( i, size ). Bevis: - Basis - i=size er trivielt, da knude nr. size må være et blad. Da if-sætningens betingelse i<=j/2, i dette tilfælde size<=size/2, ikke er opfyldt, gør heapify() intet (skadeligt!). - Skridt - Her vil der ikke ske noget, hvis ingen af børnene er større end knuden i. Man kan derfor inddele i to tilfælde: Kun ét barn: nodes[2i]>nodes[i]: Bevirker at de byttes om. Derved kommer nodes[i] til at opfylde heapbetingelsen i forhold til sit barn nodes[2i]. Da nodes[2i] ikke kan have noget barn opfylder den også betingelsen. Knuderne i+1, i+2, ... , 2i-1 holder ikke op med at opfylde heapbetingelsen, da de ikke er indvolveret. Altså opfylder i, i+1, ... , size heapbetingelsen i forhold til sine børn, da 2i nødvendigvis må være lig size, da den ellers ville have en bror. To børn: Her er situationen som ovenfor, bortset fra, at 2i ikke nødvendigvis er lig size. Med samme argument som ovenfor får vi derfor at heapbetingelsen er opfyldt for i, i+1, ... , 2i, 2i+1. Dvs. vi mangler 2i+1, 2i+2, ... , size. Når 2i<size giver induktions-hypotesen, at 2i+1, ... , size eller 2i+2, ... , size (alt efter om det er nodes[2i] eller nodes[2i+1], der er størst) opfylder heapbetingelsen i forhold til deres børn. Vi har derfor resultatet, da dette fuldender del-array'et. Q.E.D
	Man kan vise at tidskompleksiteten for arrayToHeap er O( n ) [AHU 74, s.90-91].
Arrayet delvist ordnet	På grund af heapbetingelsen bliver array'et efter arrayToHeap delvist ordnet i aftagende orden. Der er altså en vis grad af ordning, men skal vi have array'et helt sorteret må vi overskride grænsen mellem O(n) og O(n log n). Vi er derfor med arrayToHeap på vej mod grænsen mellem usorteret og sorteret fra den usorterede side.
	Efter vi nu har en heap på den ønskede array-form, vil vi se på de metoder vi ønsker i en sådan container-klasse.
	1.2 Indsættelse
Næste ledige plads	insert laves ved at placere det nye element på den næste ledige plads i array'et: nodes[size+1], og dernæst justere så heapbetingelsen igen er opfyldt. Det svarer i træet til, at det nye element placeres på den næste ledige plads i bunden af træet fra venstre mod højre, og dernæst bobler op indtil heapbetingelsen igen er opfyldt [Sedgewick 92, s.150].
	Vi får derfor:
Source 4: Overordnet indsættelses-metode	public void insert( int e ) { size++; nodes[size] = e; bobleUp( size ); }
	hvor bobleUp laves ved:
Source 5: Boble op	private void bobleUp( int k ) { int v = nodes[k]; while ( k>1 && nodes[k/2] < v ) { nodes[k] = nodes[k/2]; k /= 2; } nodes[k] = v; }
	k>1 betyder, at A[k] ikke er roden. k/2 er som bekendt faderen til k.
	Da vi konstruerede heapen med arrayToHeap, brugte vi heapify. Man føjede et nyt element til fra oven og lod det boble ned til heapbetingelsen var opfyldt. heapify var lavet rekursiv og bobleUp kan naturligvis også laves rekursiv.
Source 6: Rekursiv bobleUp	private void bobleUp( int k ) { int tmp; if ( k>1 && nodes[k] > nodes[k/2] ) { tmp = nodes[k]; nodes[k] = nodes[k/2]; nodes[k/2] = tmp; bobleUp( k/2 ); } }
	Den iterative udgave af bobleUp tager elementet ud i v og foretager derefter kun halve swaps, for først til sidst at fuldende "swappet". Den iterative vil derfor reelt være hurtigere, men de vil stadig have samme tidskompleksitet.
	1.3 Sletning
	Til at lave remove skal vi bruge bobleDown [Sedgewick 92, s. 152]:
Source 7: Boble ned	private void bobleDown( int k ) { int v = nodes[k]; while ( k <= size/2 ) { int j = 2*k; if ( j<size && nodes[j] < nodes[j+1] ) j++; if ( v >= nodes[j] ) break; nodes[k] = nodes[j]; k = j; } nodes[k] = v; }
	k<=Size/2 betyder: "k er ikke et blad". Da det altid er den største af børnene, der swappes med, bliver heapbetingelsen opretholdt i forhold til det andet barn.
	Man laver remove ved at flytte nodes[Size] op på den tomme plads, der opstår efter roden er fjernet, og den bobles dernæst nedad i heapen:
Source 8: Overordnet remove-metode	public int remove() { int r = nodes[1]; nodes[1] = nodes[size]; size--; bobleDown( 1 ); return r; }
O( log n )	bobleUp og bobleDown bruger hver O(log n), da de forløber langs en sti i heap-træet. Derfor bruger insert og remove også O(log n).
	2. Repræsenteret som tripel-linket træ
	[Mangler - må vente til en senere lejlighed]
	3. Sortering
	Når vi udtager et element fra heapen er det altid det største, og man kan dermed bruge en heap til at sortere en række elementer.
Dobbelt så lang tid som quisksort	Ved denne metode kan man opnå O(n log n), men heapsort vil gennemsnitlig tage dobbelt så lang tid som quicksort [Sedgewick 92, s.154].
O( n log n )	Da udgangspunktet for sortering altid er det samme: elementer i en tilfældig rækkefølge, bruger vi naturligvis først arrayToHeap, der tager O(n). Dernæst bruges remove n gange, altså O(n log n), eftersom remove tager O(log n). Alt i alt O(n log n) for hele sorteringen.
Sortering i samme array	Da vi gerne vil have, at sorteringen, om muligt kan foregå i ét og samme array, flytter vi det udtagne element ned på den ledige plads, som opstår i array'et efter det er justeret. På den måde kommer det største element, som vi først udtager, ned på sidste position osv.; hvorved elementerne bliver sorteret i ikke aftagende orden; hvilket generelt er vores mål ved sortering.
	Vi kan samle sorteringen i en metode [AHU 74, s.91]:
Source 9: Heap-sort	public void sort() { arrayToHeap(); for ( int i=size; i>1; i-- ) { int tmp = nodes[1]; nodes[1] = nodes[i]; nodes[i] = tmp; heapify( 1, i-1 ); } }
	Vi ser nu behovet for to forskellige metoder, der foretager en boble ned, da vi her ændrer endepunktet.
	for-løkken er en modificeret remove, til vores ønske om placeringen af det udtagne element.
	4. Prioritetskøer
	En traditionel kø behandler alle elementer lige. Elementer kommer ud i samme rækkefølge som de kommer ind, og ingen kan mase sig foran i køen.
	I visse situationer kan man have behov for en struktur, der prioriterer de indkomne elementer, så det element med højest prioritet i køen kommer først ud.
Prioritere behandling af kvæstelser	Man kunne f.eks. forestille sig en prioritetskø anvendt i forbindelse med patienter på en skadestue, hvor alvorlige kvæstelser bliver behandlet før mindre alvorlige.
	Man skal bemærke, at vi kun stiller det ene krav til prioritetskøer: at elementet med størst prioritet er det næste vi tager ud. Hvordan prioritetskøen ellers er implementeret er uden betydning for os.
	Det betyder, at en heap er som skabt til en prioritetskø, idet vi fra den altid udtager det største element; hvor størst i denne sammenhæng kunne være prioriteten.
	Prioriteskøer har mange anvendelsesmuligheder. Man kan endog lave en traditionel kø, vha. en prioritetskø ved at lade elementernes værdi være -t; hvor t er et udtryk for ankomsttidspunktet.
	Repetitionsspørgsmål
1	Hvad betyder heap?
2	Hvad er heap-betingelsen?
3	Hvorfor repræsenterer man ofte et heap-træ i et array?
4	Hvad er ulempen ved at bruge et array?
5	Hvilken ordning svarer rækkefølgen knuderne får i arrayet til mht. til træet?
6	Hvis en knude befinder sig på position i; hvor er så dens børn og fader?
7	Forklar hvordan der menes med en skov af heaps.
8	Hvad sker der når man bobler ned?
9	Hvorfor kan man optimere heapify til at starte med i = size/2?
10	Hvorfor bliver arrayet delvist ordnet efter heapify?
11	Hvad sker der når man bobler op?
12	Er det den iterative eller den rekursive udgave af bobleUp, som er hurtigst? Forklar.
13	Hvad er tidskompleksiteten for insert og remove? Forklar.
14	Hvordan kan man bruge en heap til at sortere?
15	Hvorfor er en heap god til at implementere prioritetskøer?
	Projekter
1	Lav en array-repræsentation af et træ; hvor hver knude kan have højest n børn, hvor både n og det maximale antal niveauer fastlægges ved instantieringen.
	Svar på repetitionsspørgsmål
1	hob eller dynge
2	At der for enhver knude gælder at begge børn er mindre end eller lig med knuden selv
3	Det bliver nemt at gå fra barn til fader, samt at træet relativ enkelt holdes komplet, med deraf følgende logaritmiske tidskompleksitet
4	Et array er statisk. Det skal derfor på forhånd være fastlagt hvor mange knuder der maximalt kan være i heap-træet
5	Level-order
6	Det ene barn på position 2*i, det andet på position 2*i+1 og faderen på position i/2
7	Det er en samling af træer der hver for sig er heap-træer. I heapify arbejder man med en sådan skov af heaps; hvor man dog skal bruge de index der stammer fra det sammede array.
8	Så swapper man knuden med det største af børnene. Dette fortsætter man med indtil knuden er større end begge børnene.
9	Det skyldes at halvdelen af alle knuder i et komplet træ er blade.
10	Fordi en heap er ordnet langs alle stier fra rod til blad, og at børnene til et barn altid har et større index end knuden selv
11	Man swapper knuden med faderen. Dette gøres indtil faderen er større end knuden selv
12	Den iterative er hurtigst, fordi den kan nøjes med "halve" swaps
13	Den er O( log n ), fordi de begge forløber langs en sti i træet. Da træet er komplet følger det at højden er logaritmisk.
14	Man smider alle data ind i heapen (heapify fra et array vil være bedst); hvorefter man udtager alle elementerne. Disse vil komme i ikke stigende orden, hvorved de bliver sorteret
15	Fordi man kan betragte knudernes værdi som deres prioritet. Høj værdi lig høj prioritet