©2000, Flemming Koch Jensen Alle rettigheder forbeholdt

Binære træer Opgaver

"How to recognize different types of trees from quite a long way away." - Monty Python

 

 

	Hægtede lister er ikke den eneste datastruktur, der kan opbygges med knuder og referencer. Vi skal i det følgende studere en anden meget anvendt datastruktur, hvor disse også spiller en central rolle. Det er træet.
	1. The Larch
Træer gror nedad	Vores forståelse af en træstrukturs opbygning er naturligvis med en vis parallel til træer i naturen, men der er en meget væsentlig forskel. Vi anskuer dem som groende ned fra himlen og derfor med toppen nedad. I virkeligheden burde man kalde dem rødder, men traditionen er en anden. Anvendelsen af træstrukturer til opbevaring af data bruges i mange sammenhænge. Man kender det fra stamtræer, hvor man kan beskrive sammenhænge mellem slægtninge. En anden udbredt anvendelse er organisationstræet, der beskriver en organisations opbygning.
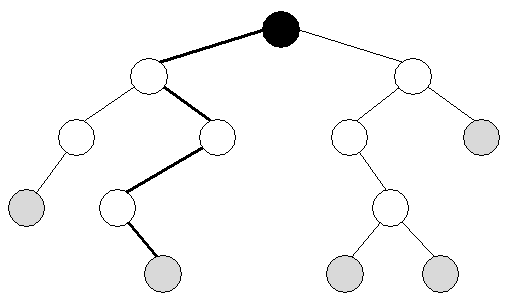
	Lad os se et træ:
Forskellige slags knuder	Man farvelægger normalt ikke et træ, som det er gjort ovenfor, men det gøres her af reference-hensyn. De runde "kugler" kaldes knuder (eng.: nodes) og stregerne kaldes kanter (eng.: edges). Den sorte knude kaldes roden (eng.: root). De grå knuder kaldes blade (eng.: leafs). Roden er kendetegnet ved, at den ikke har nogen kanter, der fører opad, mens bladene tilsvarende er kendetegnet ved, at der ikke nogen kanter der fører nedad.
Sti	I træet er markeret en række kanter. Disse kanter udgør en sti (eng.: path). En sti er en samling af kanter. Man bemærker, at der kun vil være to knuder hørende til stien, der ikke har to tilhørende kanter. Disse to knuder betegnes start- og slut-knude.
Træ	Et træ er kendetegnet ved, at der kun findes én sti mellem en vilkårlig knude og roden . Dette kan også udtrykkes som, at der kun er én sti mellem to vilkårlige knuder.
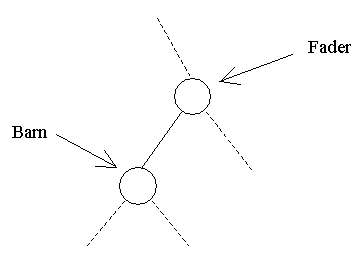
	En knude kaldes en anden knudes fader (eng.: parent), hvis de er forbundet med en kant, og faderen er tættest ved roden. Tilsvarende kaldes den anden knude for et barn (eng.: descendant eller child).
Binært træ	De træer vi vil studere, er alle kendetgenet ved, at hver knude højest har to børn. Dette gør sig f.eks. gældende for det første træ vi så ovenfor. Et træ hvor hver knude højest har to børn, kaldes et binært træ. Binært betyder som bekendt "to".
	Definition: Et binært træ Et binært træ er et træ; hvor det for hver knude i træet gælder, at det ikke har mere end to børn.
Orienteret nedad	Et træ i sig selv er ikke orienteret i nogen retning, men man vil uvægerligt se på det som startende fra roden, og derfor orienteret nedad. Man kunne derfor tegne alle kanter som nedadrettede pile i stedet for streger, men man gør det ikke.
	Når vi skal til at repræsentere træer med referencer i Java, er det denne orienterering (nedad) der bygges på. Knuder repræsenteres naturlig nok som instanser af en klasse, og kanterne vha. referencer. Vi kan stort set bruge samme klasse som for dobbelthægtede lister, men vi sætter naturligvis elementerne sammen på en anden måde:
	Node.java public class Node { protected Comparable data; protected Node left, right; public Node( Comparable data ) { this( data, null, null ); } public Node( Comparable data, Node left, Node right ) { this.data = data; this.left = left; this.right = right; } public String toString() { return "" + data; } }
null	Vi har her to referencer: left og right, der refererer til henholdsvis venstre og højre barn. Hvis en knude har færre end to børn, anvender man værdien null for manglende børn.
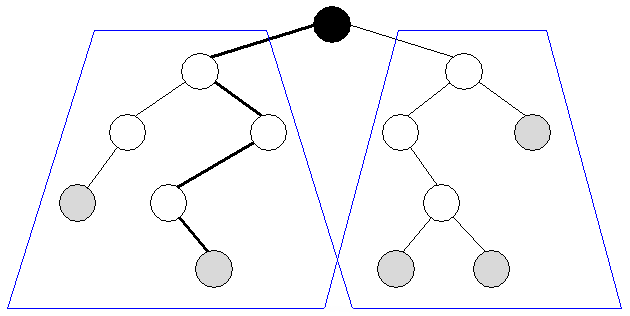
	Ser man på et træ, vil man bemærke, at det selv består af træer. Hvis vi f.eks. ser på roden i det første træ vi så ovenfor, så er dets to børn, selv rødder i hvert deres undertræ:
	Det betyder, at et træ i virkeligheden er en rekursiv struktur: Et træ består af træer!
	Man kan derfor definere et træ rekursivt:
	Definition: Et træ Et træ er enten tomt, eller består af en knude med undertræer. Et undertræ er et træ.
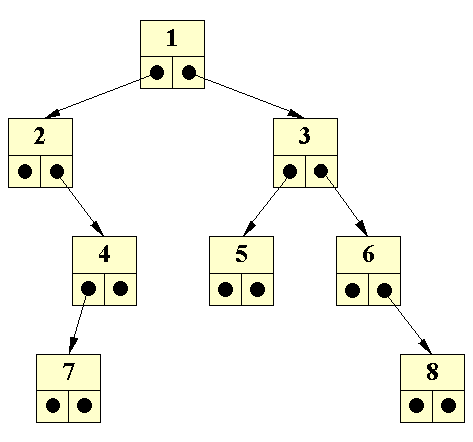
	Lad os se, hvordan er binært træ kan være opbygget med instanser af Node-klassen:
Binært træ med instanser af Node-klassen
	2. Binære søgetræer
	Vi har her ovenfor valgt at placere tallene tilfældet rundt i træets knuder, men man vil ofte ønske at værdierne er placeret efter en bestemt ordning, der gør det nemmere at søge efter dem:
	Definition: Et binært søgetræ Et binært søgetræ, er et binært træ; hvor det for enhver knude gælder, at alle knuder i dens venstre undertræ er mindre end den selv, og alle knuder i dens højre undertræ er større end den selv.
	Lad os se hvordan et sådan binært søgetræ kan se ud:
Et tilsvarende binært søge-træ
	Man ser her hvordan definitionen ovenfor, vedrørende børnenes størrelse i relation til fader-knuden, bevirker at alle knuder i et venstre undertræ er mindre end roden, og tilsvarende er alle større end roden i det højre undertræ. Dette gælde uanset i hvilken knude vi tager udgangspunkt.
	Man bemærker også en anden interessant egenskab. Når man "læser" træet fra venstre mod højre, er elementerne ordnet i ikke-aftagende orden.
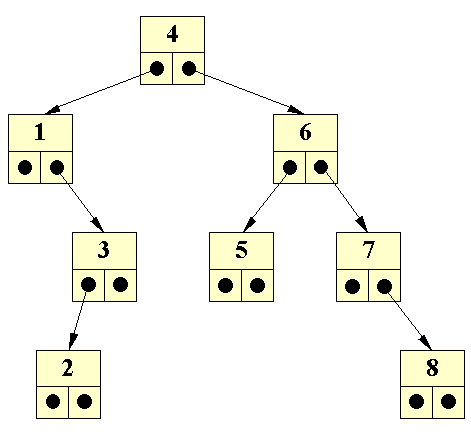
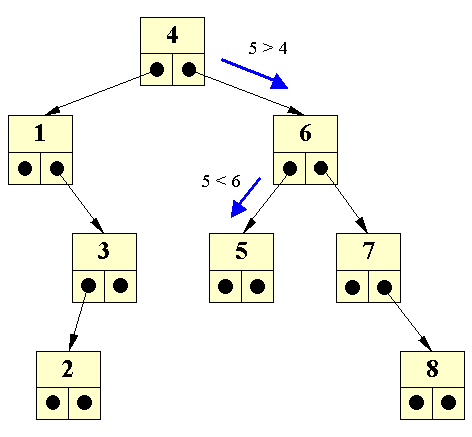
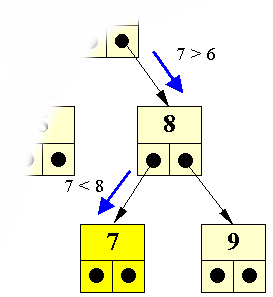
Binær søgning	Denne ordning kan udnyttes, idet man ved søgning kan navigere rundt i træet ved at sammenligne det søgte med det fundne. Hvis vi f.eks. søger efter 5 i ovenstående træ, vil vi starte i roden (hvilket vi altid gør) og sammenligne den med det søgte, nemlig 5. Da 4 er mindre end 5, kan vi udelukke at 5 skulle befinde sig i det venstre undertræ, da alle knuder i venstre undertræ vil have værdier mindre end 4. Vi går derfor ned i højre undertræ; hvor vi støder på knuden med 6. Da 6 er større end 5, kan vi udelukke at 5 skulle befinde sig i det højre undertræ, da alle knuder i 6's højre undertræ må have værdier der er større end 6. Vi går derfor ned i venstre undertræ; hvor vi netop finder 5.
Binær søgning
< >	Bemærk ulighedstegnene i de to uligheder, der er placeret ved de blå pile. Når man i ulighederne placerer det søgte forrest (i dette tilfælde 5), vil ulighedstegnet ligne en pil, der viser i hvilken retning vi skal gå!
	Ind vi se på implementationen af søgning, vil vi først se på indsættelse, da vi skal have noget at søge i.
	2.1 Indsættelse
	Hvordan skal man indsætte et nyt element i et søgetræ? Da der er tale om et søgetræ skal ordningen være bevaret efter et kald af insert-metoden.
	Hvis man, som det tidligere er nævnt, ser på søgetræet fra venstre mod højre, er det ordnet i ikke-aftagende orden. Man kan derfor slå en streg ned gennem træet, det sted hvor det nye element skal placeres i ordningen. Nederst, på en af sidderne af denne streg, må der være en knude der mangler et blad ind mod stregen. Hvorfor det?
	Hvis man betragter den sidste kant der krydser den lodrette streg, vil barnet igennem denne kant ikke have nogen efterkommere der krydser tilbage. Hvis man i dette undertræ finder den største/mindste, alt efter hvilken side vi er på, vil denne knude ikke have noget barn i den side der vender ind mod den lodrette streg. Her kan den nye knude placeres.
	Ræsonnementet er illustreret i følgende figur:
Indsættelse af 4, som blad på knude, der mangler barn ind mod stregen
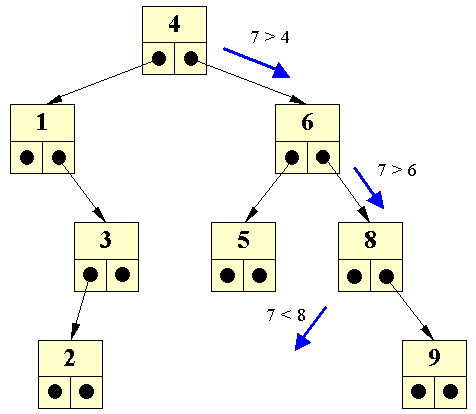
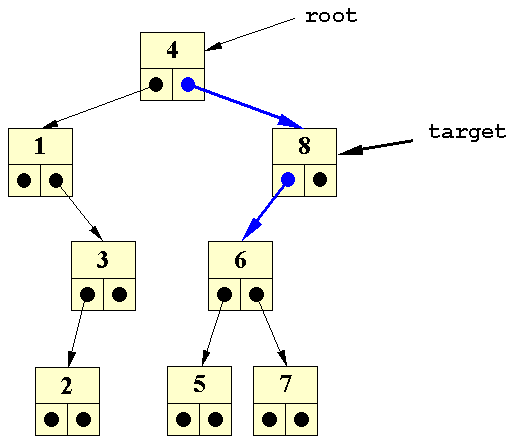
	Hvis vi foretager en mindre ændring i træet ovenfor, så 7 erstattes med 8, og 8 tilsvarende erstattes med 9, kan vi indsætte 7:
Søgning efter placering af 7
	Dette gøres ved at søge efter 7, og indsætte den nye knude det sted; hvor man ville forvente at finde 7.
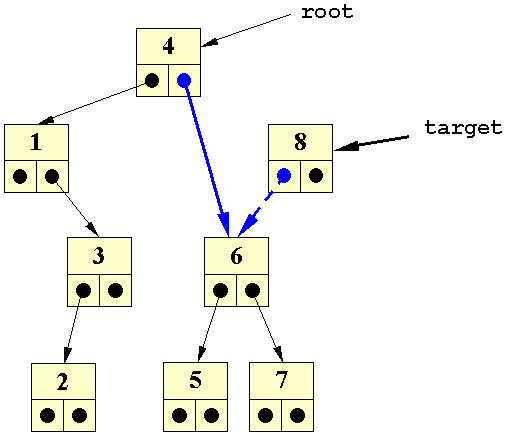
	Vi ser her, at 7 skal placeret som det venstre barn af 8:
Indsættelse af ny knude med 7
	Vi har allerede set at et træ kan defineres rekursivt. Det er derfor ikke overraskende at implementationen af indsættelse, og flere andre operationer på et træ, laves med rekursion:
	Tree.java public class Tree { private Node root; public Tree() { root = null; } /* * insert */ private static Node insert( Node subRoot, Comparable data ) { if ( subRoot == null ) return new Node( data ); if ( subRoot.data.compareTo( data ) > 0 ) subRoot.left = insert( subRoot.left, data ); else subRoot.right = insert( subRoot.right, data ); return subRoot; } public void insert( Comparable data ) { root = insert( root, data ); } ... }
Adapter-metode	Vi anvender her en adapter-metode "foran" selve den rekursive metode. Da den rekursive metode ikke direkte anvender datakernen, har vi gjort den statisk. Man bemærker, at den i stedet anvender datakernen indirekte, idet adapter-metoden sender root med som parameter.
Returnerer roden i det nye undertræ	Idéen med, at den rekursive metode returnerer roden i det nye undertræ, er at gøre det bekvemt at indsætte den nye instans af Node. I alle tilfælde, undtagen det kald hvor der instantieres en ny Node, returneres den samme Node, som blev sendt med som parameter, og der sker derfor ikke nogen ændring! Det virker umiddelbart som en masse ligegyldigt ekstra-arbejde, der alligevel ikke ændrer noget, men skal man implementere det på en anden måde, bliver indplaceringen af den nye Node-instans betydelig kompliceret.
	Bemærk, at de to if-sætninger udemærket kunne samles i en fælles if-else-else-sætning, men dette er undladt for at understrege sammenhængen mellem de to sidste situationer; hvor vi går enten til højre eller venstre.
	2.2 Søgning
	Søgning ligner på sin vis meget indsættelse. I forbindelse med indsættelse søgte vi netop efter det element vi ville indsætte, og når vi ikke fandt det, indsatte vi det der hvor vi ellers forventede det skulle have været.
	Lad os se implementationen af exists-metoden:
	Tree.java /* * exists */ private boolean exists( Node subRoot, Comparable data ) { if ( subRoot == null ) return false; if ( subRoot.data.compareTo( data ) == 0 ) return true; else if ( subRoot.data.compareTo( data ) < 0 ) return exists( subRoot.right, data ); else return exists( subRoot.left, data ); } public boolean exists( Comparable data ) { return exists( root, data ); }
	Forskellene fra insert-metoden, ligger primært i den boolske returværdi. Finder vi ikke det søgte element returnres false. Ellers checkes om vi har findet værdien; i modsat fald søges der videre i enten højre eller venstre undertræ.
	2.3 Sletning
	Sletning baserer sig også på søgning - idet man naturligvis skal have fundet det element, der skal fjernes - men dernæst skal man udføre en mere kompliceret operation.
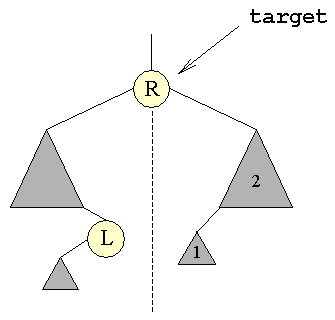
	Vi vil i det følgende betegne den knude, der indeholder det element der ønskes slettet, som: target.
Tre situationer	Når vi skal slette en knude, kan vi foretage en opdeling i tre situationer, alt efter hvor target befinder sig.
	1. target er et blad
	I denne situation fjerner man blot bladet, og sætter faderens reference til null.
	2. target har kun ét undertræ
	Er der netop ét undertræ, er situationen en anelse mere kompliceret. Lad os se et eksempel med instanser af Node-klassen:
Fjerne knude, der kun har et venstre undertræ
	Her vil vi gerne fjerne elementet: 8. Dette gøres ved at føre referencen til target udenom, og ned til target's undertræ:
Oprykning af venstre undertræ
	3. target har to undertræer
	Dette er den interessante situation, idet de to foregående har været ukomplicerede.
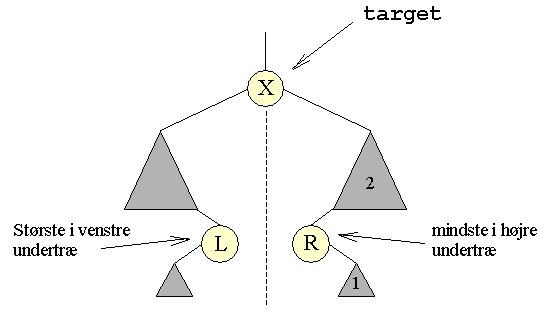
	Her skal man se på det undertræ der har target som rod. Da target har to undertræer vil der i disse være to knuder L og R, der er placeret på følgende måde:
De to kandidater: L og R, der kan erstatte X
De to værdier der er nærmest	Om L og R gælder der, at de er henholdsvis det største og det mindste element i deres respektive undertræer af target. At sådanne knuder findes, følger af vores tidligere observation, af at elementerne står i ikke-aftagende orden, læst fra venstre mod højre. Disse to knuder vil indeholde de to elementer, der kommer lige før, henholdsvis lige efter, target's værdi: X.
Ligeværdige	Både L og R er derfor ligeværdige kandidater til at erstatte target's værdi: X. Af praktiske grunde beslutter vi os for altid at bruge en bestemt af dem: R, men vi kunne lige så godt have valgt L.
	Operationen går nu ud på at flytte værdien R op i target, og slette R's oprindelige knude:
Efter R har erstattet X
Situation 2	Man bemærker at sletningen af R's oprindelige knude, svarer til situation 2, beskrevet ovenfor.
	Løsningen i situation 3 forløber derfor i to skridt: ,
	1. target skal findes 2. R's knude skal findes, X skal sættes til R, og R's oprindelige knude skal slettes
	Der er altså tale om to søgninger, og en sletning.
	Implementationen bliver som følger:
	Tree.java /* * remove */ public Comparable getR( Node node ) { // PRE: node.left != null (dvs. node har et venstre undertræ) if ( node.left.left != null ) // ser éne ekstra frem // vi skal længere ned til venstre return getR( node.left ); else { // node.left er den længst til venstre // R's data skal returneres Comparable data = node.left.data; // Hiver R's undertræ op node.left = node.left.right; return data; } } public Node remove( Node subRoot, Comparable data ) { if ( subRoot != null ) { if ( subRoot.data.compareTo( data ) < 0 ) // vi søger ned i højre undertræ subRoot.right = remove( subRoot.right, data ); else if ( subRoot.data.compareTo( data ) > 0 ) // vi søger ned i venstre undertræ subRoot.left = remove( subRoot.left, data ); else { // subRoot er 'target' if ( subRoot.right == null ) // ikke noget højre undertræ, // så vi hiver det venstre op return subRoot.left; else if ( subRoot.left == null ) // ikke noget venstre undertræ, // så vi hiver det højre op return subRoot.right; else { // to undertræer if ( subRoot.right.left == null ) { // højre barn har ikke noget venstre undertræ, // er et specialtilfælde hvor 'getR' ikke kan // hjælpe os // flytter R's data op i target subRoot.data = subRoot.right.data; // løfter højre barns højre undertræ op subRoot.right = subRoot.right.right; } else // lad os finde R subRoot.data = getR( subRoot.right ); } } } return subRoot; } public void remove( Comparable data ) { if ( root != null ) root = remove( root, data ); }
Søgning + sletning af R's knude	Vi laver her en ekstra service-metode: getR, til at finde R, og slette R's oprindelige knude. getR returnerer R - dvs. værdien fra knuden. Bemærk at denne metode må kigge to skridt fremad (til venstre), for at den kan slette R's knude når den finder den. Det kræver nemlig adgang til R's knudes fader, da denne left skal ændres.
Søgning + de tre situationer	I den første remove-metode, finder vi i starten selve søgningen (markeret med rødt), Dernæst følger de tre muligheder (markeret med blåt). Bemærk at vi er nød til at skilde et særtilfælde ud i forbindelse med sletning af target; hvis den har to undertræer, og target's højre barn ikke har et venstre undertræ.
	Den sidste remove-metode er blot en adapter-metode.
	3. Gennemløb
Traversering	Gennemløb (også kaldet traversering) drejer sig om, i hvilken rækkefølge vi besøger knuderne; såfremt vi vil besøge dem en efter en.
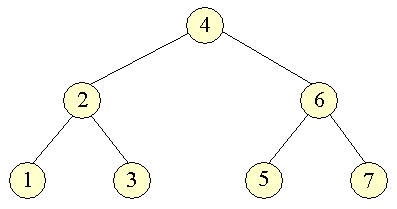
	Der findes fire former for gennemløb. Vi vil anvende følgende træ til at eksemplificere deres virkemåde:
	Vi vil illustrere de fire forskellige former for gennemløb, ved at se hvilken i rækkefølge elementerne vil blive besøgt.
	3.1 Preorder
	Et preorder gennemløb vil for hver knude der besøges, først se på knuden selv, og dernæst dens to børn (venstre først).
	Rækkefølgen vil derfor bliver: 4, 2, 1, 3, 6, 5, 7.
	Man kan generelt implementere et preorder gennemløb med følgende:
Generel preorder implemen- tation	Tree.java public void preorder( Node subRoot ) { if ( subRoot == null ) return; // knuden selv preorder( subRoot.left ); preorder( subRoot.right ); }
	3.2 Inorder
	Et inorder gennemløb vil for hver knude der besøges, først besøge det venstre barn, dernæst knuden selv, og endelig dens højre barn.
	Rækkefølgen vil derfor bliver: 1, 2, 3, 4, 5, 6, 7.
	Inorder passer derfor godt til et binært søgetræ, hvis man vil besøge knuderne i henhold til deres ordning. Dette kan f.eks. bruges i forbindelse med en toString-metode:
	Tree.java private String toString( Node subRoot ) { if ( subRoot == null ) return ""; StringBuffer sb = new StringBuffer(); sb.append( toString( subRoot.left ) + " " ); sb.append( subRoot.data ); sb.append( " " + toString( subRoot.right ) ); return sb.toString().trim(); } public String toString() { return "[Tree: " + toString( root ) + "]"; }
	Man ser tydeligt inorder gennemløbet, i den med blåt markerede del af implementationen. Bemærk, at vi ser på vores egen data, imellem de to rekursive kald til undertræerne, og at vi først går til venstre.
	Man kan generelt implementere et inorder gennemløb med følgende:
Generel inorder implemen- tation	Tree.java public void inorder( Node subRoot ) { if ( subRoot == null ) return; inorder( subRoot.left ); // knuden selv inorder( subRoot.right ); }
	3.3 Postorder
	Der skal nu ikke megen fantasi til at forestille sig, hvad der sker ved et postorder gennemløb - man ser først på børnene (venstre først) og dernæst på knuden selv.
	Rækkefølgen vil derfor bliver: 1, 3, 2, 5, 7, 6, 4.
	Man kan generelt implementere et postorder gennemløb med følgende:
Generel postorder implemen- tation	Tree.java public void postorder( Node subRoot ) { if ( subRoot == null ) return; postorder( subRoot.left ); postorder( subRoot.right ); // knuden selv }
	3.4 Levelorder
	Levelorder gennemløb adskiller sig en del fra de tre andre. I er levelorder gennemløb, besøges knuder som ville man læse dem som linier på et stykke papir - fra venstre mod højre, oppefra og ned.
	Rækkefølgen vil derfor bliver: 4, 2, 6, 1, 3, 5, 7.
	Implementationen synes umiddelbart at blive meget vanskelig, men der er et lille trick, der gør det meget enkelt - man anvender en kø!
	Hver gang man besøger en knude indsætter man dens børn i køen (venstre først), og hver gang man vil videre til næste knude, vælger man den forreste i køen.
	Idet vi anvender ListQueue-klassen, fra kapitlet: "Stakke og køer", bliver implementationen som følger:
Generel levelorder implemen- tation	Tree.java public void levelorder() { if ( root == null ) return; ListQueue queue = new ListQueue(); queue.insert( root ); while ( !queue.empty() ) { Node next = (Node) queue.remove(); System.out.print( next.data + " " ); if ( next.left != null ) queue.insert( next.left ); if ( next.right != null ) queue.insert( next.right ); } }
	Vi har her valgt at lade metoden udskrive elementerne efterhånden som de bliver besøgt.
	4. Eksempel: Split
	<Dette eksempel må vente til en senere lejlighed>