Fakultet funktionen $N!$ beregnes ved at gange $N$ med $N\!-\!1$, $N\!-\!2$, osv. ned til $1$. Lad os se et eksempel med $5!$:
Hvad kan man så bruge det til? Man kan på den måde definere fakultet rekursivt:
Fakultet
// PRE: n >= 0
int fak(int n) {
if (n == 0)
// 0! = 1
else
// N! = N * fak(N-1)
}
Rekursiv: Fakultet
// PRE: n >= 0
int fak(int n) {
if (n == 0)
return 1;
else
return n * fak(n-1);
}
Forløbet af de rekursive kald
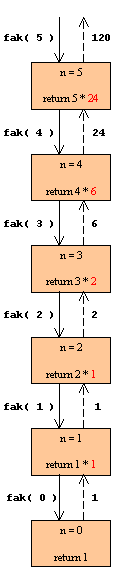
Iterativ: Fakultet
// PRE: n >= 0
int fak(int n) {
int fakultet = 1;
for (int faktor=n; faktor>0; faktor--)
fakultet *= faktor;
return fakultet;
}
Rekursiv: Fibonacci
// PRE: n >= 0
int fib( int n ) {
if (n < 2)
return n;
else
return fib(n-1) + fib(n-2);
}
Forløbet af de rekursive kald
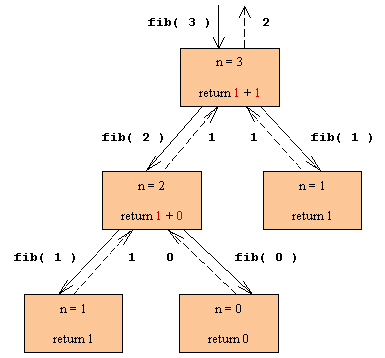
Iterativ: Fibonacci
// PRE: n >= 0
int fib(int n) {
if (n < 2)
return n;
else {
int fib2=0;
int fib1=1;
for (int i=1; i<n ; i++) {
tmp = fib1;
fib1 = fib1 + fib2;
fib2 = tmp;
}
return fib1;
}
}
Optimeret iterativ: Fibonacci
// PRE: n >= 0
int fib(int n) {
int fib2=1;
int fib1=0;
for (int i=0; i<n ; i++) {
tmp = fib1;
fib1 = fib1 + fib2;
fib2 = tmp;
}
return fib1;
}
Rekursiv: Største fælles divisor
// PRE: m >= n > 0
int gcd( int m, int n ) {
if (m % n == 0)
return n;
else
return gcd(n, m % n);
}
Forløbet af de rekursive kald
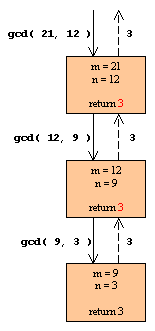
Iterativ: Største fælles divisor
// PRE: m >= n > 0
int gcd(int m, int n) {
int tmp;
while (m % n > 0) {
tmp = n;
n = m % n;
m = tmp;
}
return n;
}
Forløbet af de rekursive kald
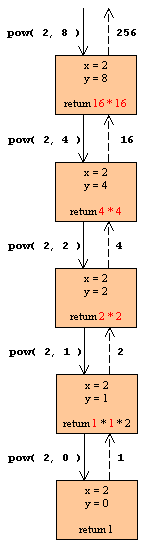
Rekursiv: Exponentiering
public class Eksponentiering {
// PRE: y >= 0
private static int pow(int x, int y) {
if (y == 0)
return 1;
else {
int halvPow = pow(x, y/2);
int fuldPow = halvPow * halvPow;
if (y % 2 == 1)
fuldPow *= x;
return fuldPow;
}
}
public static void main(String[] args) {
for (int i=0; i<=10; i++)
System.out.print(pow(2, i) + " ");
System.out.println();
}
}
1 2 4 8 16 32 64 128 256 512 1024
Matematisk rekursion
// PRE: n er okay
int rekursiv(int n) {
if (n er basis)
// basis - én eller flere mulige værdier
else
// rekursions skridt - ét eller flere rekursive kald
}
boolean palindrom(String ord)
|
$S_0 S_1 \ldots S_{n-1} S_n$ er et palindrom; hvis $S_0$ er det samme bogstav som $S_n$, og $S_1 \ldots S_{n-1}$ er et palindrom. $S_0$ er et palindrom Den tomme tekststreng er et palindrom. |
Rekursiv: Palindrom
boolean palindrom(String ord) {
if (ord.length() < 2)
return true;
else if (ord.charAt( 0 ) == ord.charAt(ord.length()-1))
return palindrom(ord.substring(1, ord.length()-1));
else
return false;
}
Forløbet af de rekursive kald
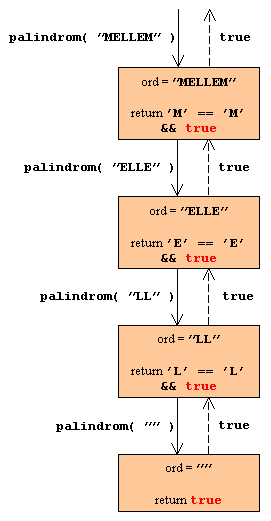
Iterativ: Palindrom
boolean palindrom(String ord) {
for (int pos=0; pos<ord.length(); pos++)
if (ord.charAt(pos) != ord.charAt(ord.length-1 - pos))
return false;
return true;
}
Towers of Hanoi med tre skiver
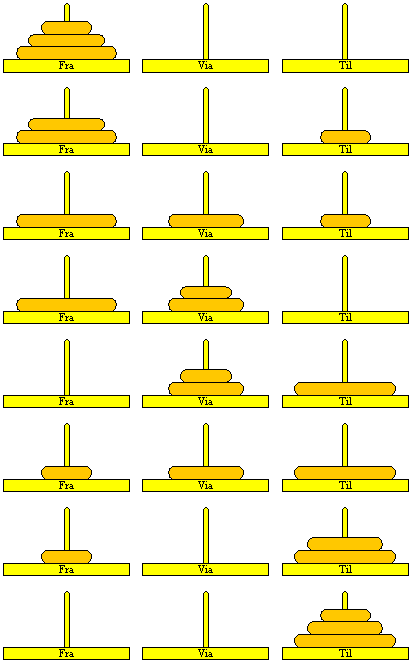
Del-problem med tre skiver
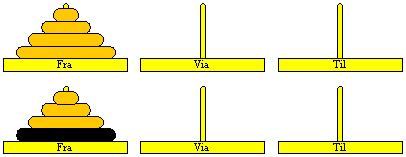
Løsning af del-problem med tre skiver

Flytning af den store skive

Løsning af del-problem med tre skiver
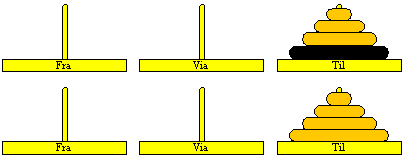
Løsning af problem med N skiver, ved løsning af to del-problemer med N-1 skiver
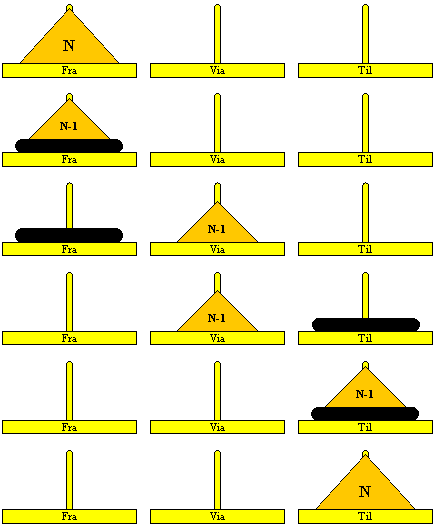
Rekursiv: Towers of Hanoi
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class Hanoi {
private static void hanoi(int antal, int fra, int til, int via) {
if (antal>1) {
hanoi(antal-1, fra, via, til);
System.out.println(fra + " -> " + til);
hanoi(antal-1, via, til, fra);
} else
System.out.println(fra + " -> " + til);
}
public static void main(String[] args) throws IOException {
BufferedReader indlæser =
new BufferedReader(
new InputStreamReader(System.in));
System.out.print("Hvor mange skiver: ");
int nSkiver = Integer.parseInt(indlæser.readLine());
hanoi(nSkiver, 1, 3, 2);
}
}
Hvor mange skiver: 3
1 -> 3
1 -> 2
3 -> 2
1 -> 3
2 -> 1
2 -> 3
1 -> 3
Rekursiv: Udskriv array
public class AdapterMetode_Eksempel {
private static void udskrivArray(int[] tabel, int pos) {
if (pos < tabel.length) {
System.out.print(tabel[pos] + " ");
udskrivArray(tabel, pos+1);
}
if (pos == 0)
System.out.println();
}
public static void main(String[] args) {
int[] t = { 5, 8, 9, 3, 6, 5, 4, 1 };
udskrivArray(t, 0);
}
}
5 8 9 3 6 5 4 1
Rekursiv: Udskriv array, med adapter metode
public class AdapterMetode {
private static void udskrivArray(int[] tabel, int pos) {
if (pos < tabel.length) {
System.out.print(tabel[pos] + " ");
udskrivArray(tabel, pos+1);
}
}
private static void udskrivArray(int[] tabel) {
udskrivArray(tabel, 0);
System.out.println();
}
public static void main(String[] argv) {
int[] t = { 5, 8, 9, 3, 6, 5, 4, 1 };
udskrivArray(t);
}
}
5 8 9 3 6 5 4 1
|
Definition: Hale-rekursiv metode En rekursiv metode er hale-rekursiv, hvis der kun optræde ét rekursivt kald i metoden, og dette kald er det sidste der udføres før metoden returnerer. |
Hale-rekusion
// PRE: parametre er okay
... haleRekursion( ... ) {
if (<ikke basis>) {
<udfør rekursions-skridt>;
haleRekursion(...);
} else {
// basis
...
}
}
Iterativ udgave af Hale-rekusion
// PRE: parametre er okay
... haleRekursion(...) {
...
while (<ikke basis>) {
<udfør rekusions-skridt>;
}
...
}
| Det skal være let at formulere løsningen | Det kommer naturligvis an på det konkrete problem man løser. I første række falder det tilbage på om problemet viser sine rekursive eller iterative egenskaber. Dette afhænger ofte af øjet der ser. |
| Det skal være let at forstå løsningen | Her forudsættes naturligvis at den der læser, forstår rekursion. Rekursive løsninger er ofte lettere at læse end iterative. Det er sjældent omvendt. I de fleste tilfælde kan det være det samme, såfremt de udviser samme enkelthed. |
| Løsningen skal være hurtig | Hvad er hurtigst? Generelt er iteration hurtigere end rekursion. Det skyldes at metode-kald tager ekstra tid at udføre. |
|
Konklusion: Man skal benytte rekursion i stedet for iteration, såfremt:
|
Repetitionsspørgsmål
Svar på repetitionsspørgsmål