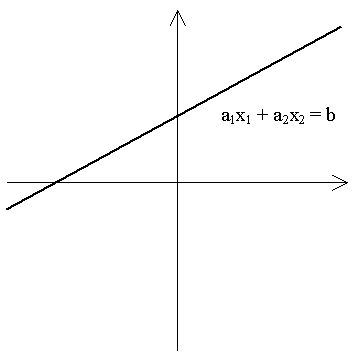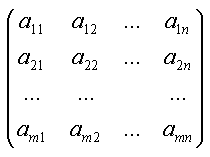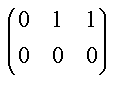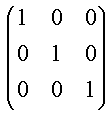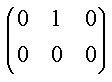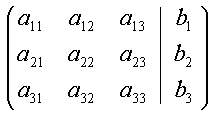© 1999-2003, Flemming Koch Jensen Alle rettigheder forbeholdt

Lineære ligningssystemer rev: 18. september 99

"..." - ...

.

Forudsætninger: .

 

 

	En lineær ligning i n variable x1, x2, ... , xn kan udtrykkes på formen:
(1)	a1x1 + a2x2 + ... + anxn = b
	a1, a2, ... , an kaldes koefficienter.
	Specielt for n=2 er der i R2 tale om liniens ligning.
Figur 1: Linie i R2
	Løsningen til ligningen a1x1 + a2x2 = b er punkterne på denne linie.
	Der gælder generelt at løsningen til en lineær ligning i Rn er en n-1 dimensional mængde. F.eks. er løsningen for en lineær ligning i R3 et plan.
	Et lineært ligningssystem består af m ligninger:
(2)	a11x1 + a12x2 + ... + a1nxn = b1 a21x1 + a22x2 + ... + a2nxn = b2 . . . . . . . . . . . . am1x1 + am2x2 + ... + amnxn = bm
	Løsningen er en mængde af n-tupler ( c1, c2, ... , cn ). Denne mængde vil have en kardinalitet på 0, 1 eller uendelig.
	Hvis vi f.eks. har et ligningssystem i R2:
(3)	a11x1 + a12x2 = b1 a21x1 + a22x2 = b2
	Vil de to ligninger beskrive to linier i planet. Hvis de er parallelle og sammenfaldende er der uendelig mange løsninger. Hvis de er parallelle, men ikke sammenfaldende er der ingen løsninger. Hvis de ikke er parallelle er der én løsning, nemlig skæringspunktet.
	Man kan bekvemt repræsentere et lineært ligningssystem med en koefficient-matrice:
(4)	=
	Eller kortere:
(5)	Ax = b
	Hvis A er kvadratisk finder man nemt løsningen som  A-1 b, da:
(6)	A-1Ax = A-1 b Ix = A-1 b x = A-1 b
	Dette forudsætter naturligvis at A ikke er singulær og dermed har en invers. I så fald er der netop denne ene løsning.
	Er A singulær eller ikke kvadratisk må man finde løsningen med en anden metode. Betragt følgende eksempel:
(7)	3x1 - 3x2 = 8 6x1 + 2x2 = 4
	Først trækker vi 2 gange den øverste ligning fra den nederste for at eliminere x1 i den nederste:
(8)	3x1 - 3x2 = 8     8x2 = -12
	Dernæst dividerer vi den nederste ligning igennem med x2's koefficient for at finde x2:
(9)	3x1 - 3x2 = 8     x2 = -1 1/2
	Endelig eliminerer vi x2 i den øverste ligning ved indsættelse af x2:
(10)	3x1 + 4 1/2 = 8     x2 = -1 1/2
	Vi har nu løsningen ( x1, x2 ) = ( 1 1/6, -1 1/2 ).
	1. Gauss-Jordan elimination
	Vi vil systematisere disse enkle ligningsoperationer i det følgende. Først vil vi dog indføre en række nyttige definitioner.
	Definition: Række-echelon1 En  matrix er på række-echelon form hvis der for enhver række gælder at: 1. Det første element (fra venstre), der er forskelligt fra 0, er 1. Dette 1-tal kaldes det ledende 1-tal. 2. At det ledende 1-tal står længere til højre end det tilsvarende 1-tal i rækken ovenover. 3. For enhver række under denne er der kun 0'er i den kolonne, hvor det ledende 1-tal står (i denne række).
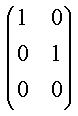
	Følgende matricer er på række-echelon form
(11)
	Definition: Reduceret række-echelon En  matrice er på reduceret række-echelon form, hvis den er på række-echelon form og der for hvert ledende 1-tal gælder at alle andre tal i rækken er 0.
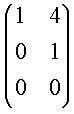
	Følgende matricer er på reduceret række-echelon form:
(12)
	For at løse et lineært ligningsystem på formen Ax = b, ønsker vi at bringe A-delen af matricen ( A b ), der opstår ved at indsætte b som en ekstra kolonne i A, på reduceret række-echelon form.
	Det kan gøres ved gentagen anvendelse af følgende række-operationer:
	1. At trække et multiplum af en række fra en anden 2. At gange en række igennem med en skalar 3. At bytte om på to rækker
	De to første kende vi allerede som lignings-operationer, mens den sidste vedrører selve række-echelon formen.
	Kan vi bringe A-delen af ( A b ) på reduceret række-echelon form vil løsningen kunne aflæses som den sidste kolonne. F.eks.:
(13)
	bringes på formen:
(14)
	Den skitserede løsningsmetode kaldes Gauss-Jordan elimination og kan konkretiseres med følgende algoritme; hvor de tre række-operationer anvendes på systematisk vis:
Pseudo 1: Gauss-Jordan elimination	1. i = 1 2. Hvis aii = 0 så: Hvis der findes en række j, hvor om det gælder at aji er forskellig fra 0 så: Byt om på række i og j Ellers Terminer (uden at reduceret række-echelon form er opnået) 3. Hvis aii er forskellig fra 1: Divider række i med aii 4. For alle j forskellig fra i: træk aji gange række i fra række j 5. Hvis i = n eller i = m: Terminer (med reduceret række-echelon form opnået) 6. i = i + 1 7. gå til 2
	Som det ses af skridt 2, vil algoritmen ikke altid terminere med en reduceret række-echelon matrice. Dette er ikke ensbetydende med at der ikke findes nogen løsninger.
	2. Gauss elimination
	3. Implementation i class Matrix
	Gauss-Jordan og Gauss elimination implementeres med to metoder i class Matrix. Metoderne adskiller sig kun ved det algoritmiske forløb. Derfor er der en del fællestræk:
	Begge metoder:
	Tager som parameter vektoren b og returnerer løsnings-vektoren c. Hvis der ikke er nogen løsninger returneres null, og hvis der er uendelig mange løsninger kastes en exception. Lave en ny instans af Matrix som ødelægges under eliminationen. Derved skånes datakernen for ændringer. Af samme grund er begge metoder static.
	De to metoder er adapter-metoder, der kalder en fælles service-metode elimination med en parameter der angiver hvilken elimination der ønskes. Metoden laver den fælles opsætning og kalder, afhængig af parameteren, én af to metoder, der implementerer det specifikke for hver af de to former for elimination. På den måde minimeres koderedundansen.
fodnoter:
1	I gamle dage udkæmpede man krige ved at de to hærer stillede op i en lang række, skulder ved skulder. Dernæst begyndte de at marchere mod hinanden. Når de var inden for skudafstand stoppede de op og begyndte at skyde indtil den ene hær var væk. Den tilbageblevne hær havde vundet. Alternativt kunne man fortsætte marchen mod hinanden og udkæmpe slaget med sabler og baronetter. Denne form for angreb kaldtes linieangreb.
	Echelon er en alternativ formation hvor man laver en forskudt linieopstilling:
Figur X: Partielt linieangreb med echelon formation
	Med denne formation skulle man være mindre sårbar overfor modangreb på flankerne; hvilket var det rene linieangrebs største svaghed.
	Hvis man sammenligner med en række-echelon matrice sporer man den lighed, der har givet navn til formen.