|
© 1999-2003,
Flemming Koch Jensen
Alle rettigheder forbeholdt |
| Grafer Opgaver |
|
Abstract: Først gennemgås de mange definitioner. Dernæst to eksempler på anvendelser: Euler stier og De Bruijn sekvenser. At finde korteste sti er det største emne med Moores, Dijkstras, Fords og Floyds algoritmer. Minimalt udspændende træ med prioritet-først søgning og Kruskals algoritme. Dybde-først søgning tager udgangspunkt i labyrinter og Trémaux' algoritme gennemgås. Repræsentationen af grafer præsenteres, mens en implementation må vente til senere. |
|
Forudsætninger: Kendskab til træer, arrays og linkede lister. Der er en række kommentarer, der kræver kendskab til tidskompleksitet, pre- og postconditions, heaps og mængdelære. |
| 0. Definitioner | ||
|
Vi har allerede set grafer i form af træer. Træer er en speciel gruppe af grafer. Lad os se definitionen på en graf og senere vende tilbage til hvad der gør træer specielle. | ||
| Graf |
| |
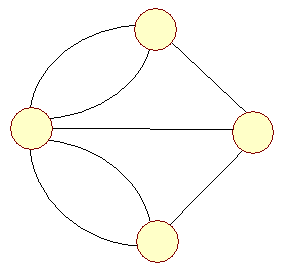
| Nogle definitioner er mere informative end andre. Ovenstående må siges at høre til de mere ugennemskuelige, så lad os i stedet se et eksempel på; hvordan en graf kan se ud: | ||
|
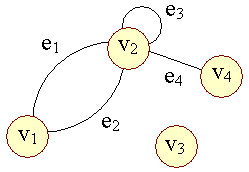
Figur 1: |
| |
| Løkke |
Man bemærker at de to knuder u og v ikke behøver at være forskellige knuder, som det ses for v2 med kanten e3. En sådan kant kaldes en løkke (eng.: self-loop). | |
| Isoleret |
Knuden v3 kaldes en isoleret knude, da den ikke har nogen kanter, og dermed er uden kontakt med andre knuder. Selv om en knude er isoleret, er den alligevel en del af grafen! | |
| Parallelle |
e1 og e2 kaldes parallelle kanter, da de forbinder de samme to knuder. | |
| Grad |
En knude e's grad: d(e) er det antal forbindelser den har til kanter. I figur 1 er: | |
| ||
| Man observerer, at en knude med grad 0 er isoleret. | ||
|
Da hver kant bidrager til den samlede graf med 2 grader vil summen af alle grader være lige, hvorfor man kan udtrykke denne sum som: | ||
|
| ||
|
Da en lige sum af en række tal forudsætter, at der er 0, 2, ... ulige tal i talrækken, har vi flg. sætning: | ||
|
| ||
| Sti |
| |
| Uformelt | Igen er den formelle definition ikke så let at gennemskue. Man kunne formulere den mere uformelt, som: En sti er en samling af kanter der forbinder kanter med hinanden som en lang "kæde". | |
| Længde |
Længden af en sti er antallet kanter. u kaldes startknuden på stien P, hvor e1 = (u, v) og v er fælles med e2 . v kaldes slutknuden på stien P, hvor ek = (u, v) og u er fælles med ek-1 . | |
|
I vores eksempel er e1, e4 en sti hvor v1 er startknuden og v4 er slutknuden. En sti må godt indeholde løkker, hvorfor man kan lave en sti, med vilkårlig længde, vha. v2: e2, e3, ... , e3, e4 . | ||
| Cycle |
En sti, hvor startknuden er den samme som slutknuden kaldes en cycle. | |
| Simpel |
En sti kaldes simpel, hvis ingen knuder optræder mere end en gang på stien. En cycle kaldes simpel hvis start- og slutknude er den samme, men stien iøvrigt er simpel. | |
| Sammen- hængende |
En graf kaldes sammenhængende, hvis der for alle knudepar i grafen eksisterer en sti, hvor disse er start- og slutknude. Mao.: uanset hvilken knude man vælger, så kan man komme til enhver af anden knude via en sti. | |
|
0.1 Orienteret graf | ||
| Orienteret |
| |
|
Lad os betragte følgende orienterede graf: | ||
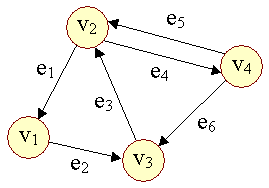
| Figur 2: Orienteret graf |
| |
|
En orienteret sti er en sti hvor ei's slutknude er ei+1's startknude og e1 ikke er em . En orienteret cycle er en orienteret sti, hvor start og slutknude er den samme. | ||
| Stærkt sammen- hængende |
En orienteret graf kaldes stærkt sammenhængende, hvis der for alle knudepar (u, v) findes en orienteret sti fra både u til v og fra v til u. Der skal altså findes en sti begge veje! | |
| Anti-parallelle |
Parallelle kanter, der er orienteret modsat hinanden kaldes antiparallelle. I figur 2, er e4 og e5 antiparallelle. | |
| Ind/ud-grad |
Udgraden dout(v) af en knude v er antallet af kanter, der har v som startknude. Indgraden din(v) af en knude v er tilsvarende antallet af kanter, der har v som slutknude. Der gælder naturligvis, at den samlede udgrad og indgrad, for en graf, er lig hinanden: | |
|
| ||
|
Når man skriver graf, mener man en ikke-orienteret graf, med mindre andet fremgår af sammenhængen. Ved orienterede grafer bruger man ofte at betegne dem som dgrafer (d: directed), men i tale bruger man stadig betegnelsen orienteret graf. | ||
|
0.2 Vægtet graf | ||
| Vægtet |
| |
| Den numeriske størrelse vil i dette kapitel altid være et heltal, men det kunne f.eks. også være et kommatal, eller endog et komplekst tal! | ||
| Lad os et eksempel på en vægtet graf: | ||
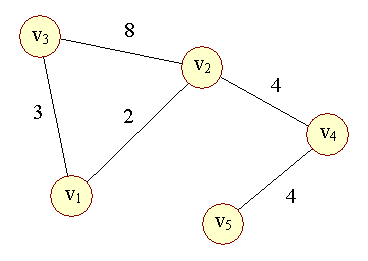
| Figur 3: Vægtet graf |
| |
|
0.3 Træ | ||
|
Efter at have defineret en lang række betegnelser vi skal bruge i forbindelse med grafer, er det nu muligt præcist at beskrive, hvilken gruppe af grafer, der kan betegnes som træer. | ||
| Træ er graf |
| |
| Skov |
Hvis man fjerner kravet om, at grafen skal være sammenhængende får man i stedet en samling af træer. En sådan graf kaldes en skov. | |
| Man kan på samme måde definere et binært træ ud fra graf-begrebet: | ||
| Binært træ |
| |
| Roden | Sidstnævnte knude, med grad på højest 2, skal eksistere, da roden ikke må have en grad større end 2. Roden kan derfor kun vælges blandt de knuder har en grad på højest 2. | |
| Bemærk i øvrigt, at det ikke er muligt at lave en graf med ene knuder der har grad 3, uden at der opstår cycler. Dermed er det sidstnævnte krav, mere en konstatering, end det er et krav i sig selv! | ||
|
Inden vi går videre, med den generelle grafteori, vil vi se på to interessante anvendelser af grafer. | ||
|
1. Euler-grafer | ||
|
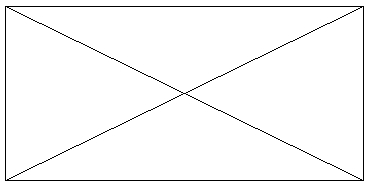
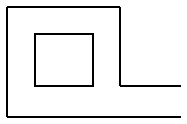
Der findes en type opgaver af formen: "Tegn, uden at løfte blyanten, og uden at lave en streg mere end én gang". F.eks. figuren der ligner en kuvert. Kan det lade sig gøre? | ||
| Figur 4: Kuverten |
| |
|
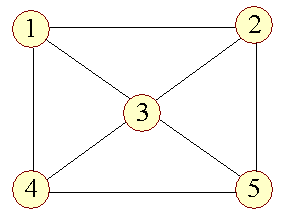
Man kan repræsentere kuverten vha. en graf, hvor alle liniestykker er kanter og alle ende/kryds-punkter er knuder: | ||
| Figur 5: Graf for kuverten |
| |
| For at kunne besvare spørgsmålet skal vi først se på Euler-stier og bevise en sætning. | ||
| Euler-sti |
En Euler-sti er en simpel sti uden løkker, der har samme længde som antallet af kanter i grafen. Derfor vil alle kanter i grafen være repræsenteret én gang i stien. | |
| Euler-graf |
En graf med en Euler-sti kaldes en Euler-graf. Til at afgøre om en graf er en Euler-graf kan man bruge følgende kraftfulde sætning: | |
|
| ||
|
Hvis der ikke er nogen knuder af ulige grad vil Euler-stien være en Euler-cycle, ellers ikke | ||
|
| ||
|
Den algoritme, der er skitseret i bevist for sætningen, har en tidskompleksitet på O(|E|), hvilket ikke kan overraske nogen. | ||
| Kuverten dur ikke |
Vi kan nu bruge sætningen til at svare på spørgsmålet, om man kan tegne kuverten uden at løfte blyanten eller tegne en streg mere end en gang. Kuverten har fire knuder af ulige grad, og den er derfor ikke en Eulergraf. Det er derfor ikke muligt! | |
|
Det store klassiske eksempel på anvendelsen, er et virkeligt problem, som man grublede over i gamle dage: "Königsberg broerne". | ||
|
Euler blev engang udfordret af en af sine venner til at bevise om han kunne gå sin daglige tur i Königsberg uden at gå af en gade to gange. Han gik altid forbi de samme palæer og over de samme broer. | ||
|
Gaderne og broerne kunne repræsenteres med følgende graf: | ||
| Figur 6: Königsberg broerne |
| |
|
Som det ses har alle palæer ulige grad. Altså er det umuligt! | ||
|
Man kan også tale om Euler-grafer i forbindelse med orienterede grafer. | ||
| Orienteret Euler-sti |
En orienteret Euler-sti er en orienteret sti, hvor alle kanter i den orienterede graf optræder netop én gang. En orienteret graf er en orienteret Euler-graf, hvis den har en orienteret Euler-sti eller -cycle. | |
|
2. De Bruijn sekvenser | ||
|
De Bruijn sekvenser er et andet sofistikeret problem. Vi kender nok alle opgaven med at finde skjulte ord i en sætning, som f.eks. ordet "tand" i første linie ( ... er et andet ... ). Vi vil dog drive legen til det yderste og vende den på hovedet: At konstruere sekvenser, hvori der indgår en række tal. | ||
|
Lad S = { 0, 1, ... , m-1 } være et alfabet, dvs. de tegn vi må bruge i vores "ord", der tydeligvis bliver ciffer-sekvenser. | ||
|
Kombinatorikken fortæller os, at man med et sådant alfabet kan lave mn ord med længden n. | ||
|
| ||
| Cirkulær sekvens |
En sekvens skal forstås som en cirkulær sekvens. Det første element a0 følger efter det sidste element ak-1 . i kan derfor godt være større end n-i-1, idet man blot starter forfra med de efterfølgende tegn. Dette kan gøres ved at regne alle index som modulus k. | |
|
Vi vil se nærmere på alfabetet S = { 0, 1 }. | ||
| Hjælpe-graf |
Når vi skal konstruere en De Bruijn sekvens til dette alfabet for en given ordlængde n, vil vi bruge en orienteret graf Gn = (V, E), hvor V og E er givet ved: | |
|
| ||
|
Man ser at |V| = 2n-1 og |E| = 2n , og dermed |E| = 2 |V|. | ||
|
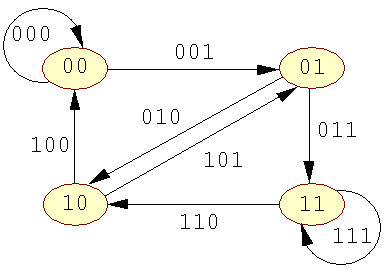
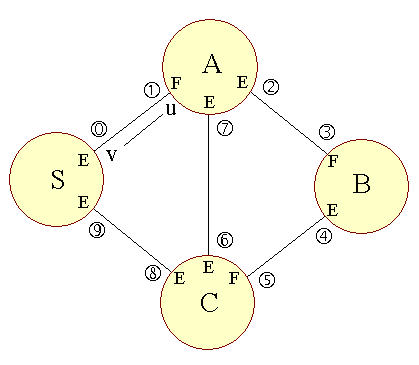
I følgende figur, ses grafen for n = 3: | ||
| Figur 7: De Bruijn-graf for n=3 |
| |
|
Man kan vise, at Gn altid vil have en Euler cycle. Dette gælder også for alle andre S end { 0, 1 }. | ||
|
Lad os finde en Euler cycle: | ||
|
| ||
|
Denne række af 24 bit er naturligvis en De Bruijn sekvens, men vi kan forkorte den betydeligt. | ||
|
Hvis vi beholder det midterste ciffer fra hver af disse kanter, og fjerner kommaerne, får vi: | ||
| De Bruijn sekvens |
| |
|
hvilket stadig er en De Bruijn sekvens for { 0, 1 } for ordlængden 3. Hvorfor det? | ||
|
Det at finde et vilkårligt ord med længde 3, er det samme som at vælge en kant i G3 , f.eks. 010. Vi fjernede ovenfor de to 0'er og bibeholdt 1. Hvordan kan vi være sikre på, at der stadig vil findes et 010, er et spørgsmål om vi kan være sikre på, om der var en kant x0x før og en kant x0x efter i vores Euler cycle. Kanten 010 starter i 01 og alle kanter der gå til 01 må naturligvis være af formen x01, hvilket tilfredsstiller x0x før. x0x efter, får vi analogt af tilknuden 10 for kanten 010. | ||
|
Man ville have fået en De Bruijn sekvens uanset om det, som her er det midterste tegn, eller det i stedet var det første eller det sidste tegn man havde valgt at beholde. Man skal i den forbindelse bemærke, at man får denne samme cirkulære sekvens, uanset hvilken man beholder. | ||
|
Hvis man går så vidt som til at vælge en anden Euler-cycle, dvs. kanterne i en anden kombination, får man en rigtig ny De Bruijn sekvens. Antallet af mulige De Bruijn sekvenser er derfor lig antallet af mulige Euler-cycler i grafen. | ||
|
3. Korteste sti | ||
|
At finde den korteste sti mellem to vilkårlige knuder i en graf, er det klassiske problem inden for grafalgoritmer. | ||
|
Der findes en del forskellige algoritmer til at løse denne opgave, og vi vil i det flg. se nærmere på en række af dem. | ||
|
3.1 Moores algoritme | ||
| Mærke knuder |
Den første er af E.F. Moore [Moore57]. I hans algoritme skal man kunne mærke alle knuder med en værdi. Som udgangspunkt er alle knuder dog umærkede. | |
|
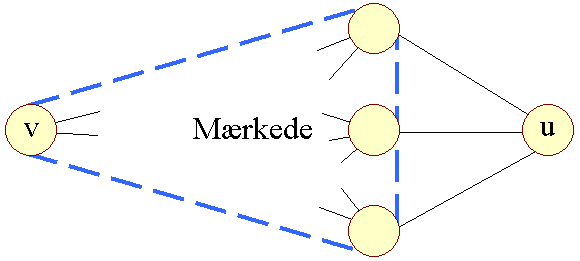
Lad os først illustrere den idé, der ligger bag. Betragt følgende figur: | ||
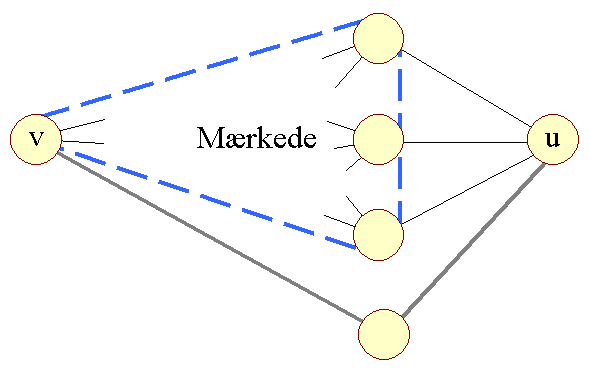
| Figur 8: u i næste skridt |
| |
|
Antag, at vi vil finde den korteste sti mellem knuderne v og u. Antag ligeledes, at en knudes mærke er længden af den korteste sti mellem v og den pågældende knude. | ||
|
I figur 8 illustrerer trekanten alle de knuder vi har mærket. v selv er naturligvis mærket med 0. De tre knuder der allerede er mærkede og som samtidig er naboer til u, er også vist. Endelig er u, som vi skal til at mærke, vist. Alle andre knuder, der endnu er umærkede, er ikke vist. | ||
|
Når vi skal fra v til u har vi to muligheder. Enten kan vi gå via de mærkede gennem de tre viste naboknuder, der også er mærkede, eller vi kan gå en anden vej! Den sidste mulighed er svær at håndtere, fordi der er så mange muligheder. Man kan gå via de mærkede til de umærkede, tilbage igen og rundt på mange måder, før man når til u. Lad os se. hvor galt det kunne se ud. Betragt følgende figur: | ||
| Figur 9: Genvej fra v til u |
| |
|
Vi ser her, at der findes en sti mellem v og u med længden 2. Vi kan derfor ikke bruge de tre andre naboknuder til u, da de vil give en længere vej (antager vi). | ||
| Forhindre genveje |
Vi vil gerne fjerne disse muligheder, så det kun er muligt at gå gennem de mærkede, via de tre naboknuder til u. Det er ikke så vanskeligt at gennemtvinge denne forenkling. Det gøres ved at sikre sig, at der ikke findes umærkede genveje til de knuder, der som u, er naboer til mærkede knuder. | |
| Afstand målt på stilængden |
Det gøres ved afstandsmæssigt (målt på stilængde) at fjerne sig fra v et skridt af gangen for alle stier der leder bort fra v. Det vil i praksis sige, at man mærker alle naboer til de allerede mærkede knuder "på en gang". Når vi mærker en ny knude, regner vi derfor ikke de nye naboer for naboer, før vi er færdig med at mærke de andre "gamle" naboer. | |
| Ringe i vandet |
De mærkede knuders andel kommer derfor til at sprede sig som ringe i vandet. | |
|
Den første knude vi mærker er naturligvis v selv; og den starter derfor med at udgøre de mærkede. Dernæst mærkes alle naboer til v. Dernæst de nye naboer osv. Hvis man vil finde den korteste sti til u, stopper man når u mærkes. Hvis man først stopper når alle knuder er mærkede, har man alle korteste stier fra v til alle andre knuder. | ||
|
Det følger her af, at Moores algoritme ikke har den store prisforskel mht. om man vil finde den korteste sti til én knude eller dem alle. Tidskompleksiteten er den samme, da vi i værste tilfælde først finder v som den sidste knude. I snit vil det dog tage dobbelt så lang tid at finde alle korteste stier. | ||
|
Lad og se algoritmen: | ||
| Pseudo 1: Moores algoritme |
| |
|
Hvis man vil finde alle korteste stier fra v til alle andre knuder i grafen, skal man blot udelade skridt 5. | ||
| Nemt at finde korteste sti ud fra mærkerne |
Vi har flere gange sagt, at Moores algoritme finder den korteste sti mellem u og v, men hele tiden beregnet længden af den korteste sti! Denne tilsnigelse er ikke noget problem, da man trivielt kan finde en korteste sti når man først har mærkerne. Man går nemlig fra u tilbage mod v, ved hver gang at vælge den naboknude, der har det mindste mærke; altså i vores tilfælde knuder, der er mærket én mindre end den vi står i! Hvis der findes flere korteste stier mellem v og u, vil dette give sig til kende ved, at man på vej tilbage må vælge mellem flere knuder med samme mindste mærke. | |
|
3.1.1 Ringe i vandet | ||
| Når man beskriver Moores algoritme, kan man også vælge at se på den som en proces, der spreder sig som "ringe i vandet". | ||
| Betragt følgende figur: | ||
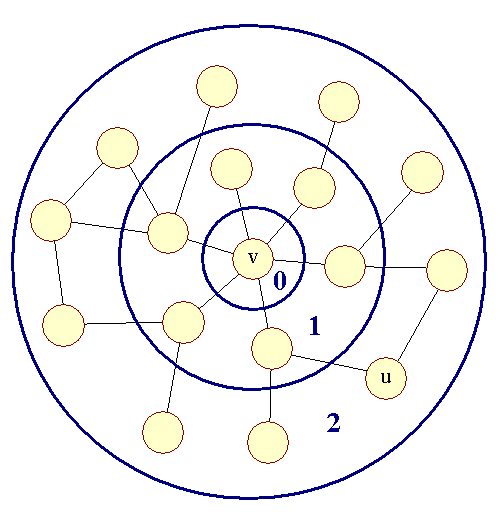
| Figur 10: Ringe i vandet |
| |
| Hvis man rykker lidt rundt på knuderne i en graf kan man få den til at bredde sig ud som ringe, idet man indenfor hver ring placerer knuder med samme afstand til udgangspunktet v. Kanter vil kun gå mellem knuder i to nabo-cirkler eller internt mellem knuder i samme cirkel. Det er denne obervation, der ligger bag Moores algoritme, den spreder sig ud gennem grafen som "ringe i vandet". | ||
|
3.1.2 Begrænsninger | ||
| Orienterede grafer |
Kan algoritmen bruges på orienterede grafer? Det er der ingen problemer i. Man skal naturligvis kun se på de naboknuder til de mærkede, som har en kant fra en af de mærkede. | |
| Ikke til vægtede grafer |
Kan algoritmen bruges på vægtede grafer? Nej, det kan den ikke. Moores algoritme er afhængig af, at alle kanter har samme længde, så en sties længde er proportional med antallet af kanter. Følgende figur illustrerer, hvilken situation der kunne opstå: | |
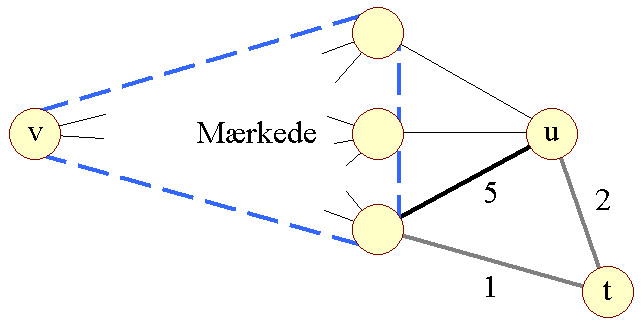
| Figur 11: Moores algoritme og vægte |
| |
| Kortere omvej |
Her vil den direkte vej være den længste (5), mens "omvejen" via t vil være den korteste (1+2 = 3 < 5). | |
|
Tidskompleksiteten for Moores algoritme er O(|E|), da vi i worst case skal mærke alle knuder; hvilket kræver, at vi inspicerer alle kanter i skridt 3. | ||
|
Vi skal senere, under dybde-først søgning, vende tilbage til Moores algoritme og kalde den bredde-først søgning. | ||
|
Moores algoritme virkede som nævnt ikke for vægtede grafer. At finde den korteste sti mellem to knuder v og u er en sværere opgave i vægtede grafer. Vi må derfor konstruere en anden algoritme, og måske være forberedt på, at det kommer til at koste i tidskompleksiteten! | ||
|
3.2 Dijkstras algoritme | ||
|
I eksemplet, hvor vi demonstrede, at Moores algoritme ikke fungerede med vægtede grafer, var problemet, at en omvej kunne vise sig at være kortere. Vi ville i figur 11 fejlagtigt mærke u baseret på kanten med længde 5, i stedet for det rigtige: 3. Hvis vi leger lidt videre med tanken ser vi, at fejlen ikke vil blive "opdaget", da u nu vil høre til de mærkede og derfor aldrig blive ændret. Fejlen ville få mulighed for at forplante sig videre. Hvis vi derfor skal tage udgangspunkt i Moores algoritme, må vi i det mindste opgive, at de mærkede knuder skal forblive uændrede! | ||
|
Men hvilke knuder skal vi så inspicere? Når vi først har brugt en knude, som f.eks. t, til at fortælle en anden knude, f.eks. u, at dens mærke (midlertidigt) skal være en bestemt værdi, vil vi udelukke den fra at "komme til orde" igen. Det vil være en måde at tvinge algoritmen frem mod terminering, ved at bringe knuder "ud af spillet", men går det godt? | ||
|
Det problem, der kan opstå ved, at en knude bringes ud af spillet, men stadig kan ændre mærke, er de "fejlagtige" oplysninger, der er givet videre til dens naboer. Hvis f.eks. t's mærke bliver ændret, kan den ikke bringe meddelelsen videre til u, om at dén nu kan tilbyde en endnu kortere sti! | ||
| Tage knuden med mindst mærke |
Løsningen er at hindre en sådan senere kortere sti i at forekomme. Hvis en kortere vej skal opstå hen mod u, må der være andre knuder med mindre mærker, der stadig er med i spillet, og som kan fortælle t, at der nu er en kortere sti. For at forhindre dette sker, må vi altid tage den knude med mindst mærke, der endnu er med. | |
|
Denne algoritme er udtænkt af Dijkstra [Dijkstra59]. Lad os se den konkretiseret: | ||
| Pseudo 2: Dijkstras algoritme |
| |
|
Bemærk, at man i skridt 3 ikke kan vælge en umærket knude! | ||
|
Igen er skridt 4 eller mangel på samme afgørende for, om vi finder korteste sti mellem v og u, eller mellem v og alle knuder i grafen. En anden lighed er derfor den begrænsede forskellighed i de to opgavers tidsforbrug. | ||
|
Tidskompleksiteten for Dijkstra algoritme er O(|V|2), og dermed en forudsigelig prisstigning. Det vi hermed har opnået er altså at finde korteste sti for vægtede grafer. Det for såvel orienterede som almindelige. | ||
|
Der er dog en detalje i vores ræsonnement vedr. Dijkstras algoritme, vi gik let hen over: Vægtene må ikke være negative. | ||
| Antog at en kant mere, gjorde stien længere |
Problemet ligger i, at vi ved negative vægte ikke kan være sikre på, at knuden med mindst mærke i T har det endelige mærke. Det kan være der findes en negativ vej vi endnu ikke har mødt som gør en anden sti kortere. Det skyldes med andre ord en antagelse om, at summen af kanter på en sti er større end eller lig de individuelle kanter. Dvs. en kant mere på en sti gør den længere eller lige så lang. | |
|
3.3 Fords algoritme | ||
|
Hvis vi fjerner den løbende udelukkelse af kanter fra Dijkstras algoritme får vi Fords algoritme [Ford56]: | ||
| Pseudo 3: Fords algoritme |
| |
|
Da Fords algoritme ikke bringer nogen knuder ud af spillet, lider den ikke af den skavank vi fandt i Dijkstras algoritme. | ||
| Ikke med negative cycler |
En fordel ved at indføre det fænomen, at knuder "blev sat ud af spillet", var at presse algoritmen frem mod terminering. Dette tryk er nu væk! Kan vi over hovedet være sikre på, at algoritmen terminerer? Nej! Hvis der findes en cycle med negativ længde vil algoritmen blive ved at "køre rundt" i den. | |
|
Man kan vise, at tidskompleksiteten for Fords algoritme er O(|E||V|); hvis man udfører skridt 2 ved at gennemsøge kanterne i samme rækkefølge hver gang. Som ventet er tidskompleksiteten for Fords algoritme dårligere end Dijkstras, da der ikke er det samme pres frem mod terminering. | ||
|
Igen, der er et problem! I en ikke-orienteret graf vil en negativ kant have samme virkning som en negativ cycle, da man kan gå frem og tilbage på den. | ||
|
Vi kan altså godt bruge Fords algoritme på orienterede grafer med negative kanter, men mangler skridtet helt ud. Igen, det kommer til at koste! | ||
|
Vi vil som med Dijkstras algoritme lave en inkrementerende løsning, og dermed få et pres frem mod terminering. | ||
|
3.4 Floyds algoritme | ||
|
Lad V = { v1, v2, ... , vn }. Vi vil definere d k(s, t), k>0, som længden af den korteste sti mellem s og t, blandt de stier mellem s og t, der kun indeholder kanter fra { v1, v2, ... , vk }, men ikke { vk+1, ... , vn }. | ||
|
For k=1 er d k(s, t) længden af kanten mellem s og t, hvis en sådan eksisterer, ellers ¥ . | ||
|
Nu er det bare at starte med k=0 og så iterativt arbejde den op til n: | ||
| Pseudo 4: Floyds algoritme |
| |
|
Idéen i skridt 2 er, at enten er den korteste sti stadig den vi havde før, eller det er muligt at lave en kortere gennem den nye knude vk . | ||
|
Algoritmen kaldes Floyds algoritme [Floyd62]. | ||
| Terminerer trods alt |
d k(s, t) er kun længden af den korteste sti, hvis der ikke er negative cycler, men den terminerer trods alt! At der er negative cycler ses efterfølgende ved, at d k(i, i) < 0. Floyds algoritme bringer os op i en tidskompleksitet på O(|V|3). | |
|
4. Minimalt udspændende træ | ||
|
| ||
|
Som antydet kan der eksistere mange sådanne udspændende træer for en given graf. | ||
| Minimalt |
Det træ, der har den mindste samlede længde af kanter, kaldes det minimalt udspændende træ for G. Igen, der kan være flere af disse minimalt udspændende træer! | |
|
Der findes en del algoritmer til at finde det minimalt udspændende træ. Vi vil se på nogle af dem. | ||
|
4.1 Prioritet-først søgning | ||
|
Den første kaldes prioritet-først søgning [Sedgewick92] s.454-57. | ||
|
Da alle knuder fra grafen skal være i træet, kan vi vælge en vilkårlig knude v og tage udgangspunkt i den. | ||
| Vælg kanten med mindst længde til nabo |
Der må nødvendigvis være en kant fra v; hvorfor vi med sikkerhed kan sige at den skal forbindes med en af sine naboer. Det minimalt udspændende træ for resten af grafen, dvs. G' = (V-v, E), vil indeholde alle naboerne til v. Det minimalt udspændende træ må derfor være det minimalt udspændende træ for G', sat sammen med v vha. den mindste kant mellem v og dens naboer! Vi er derfor, den anden vej, i stand til at sige, at vi skal fortsætte fra v, ved at føje den mindste kant fra v til vores delløsning. Delløsningen indeholder nu to knuder og en kant: v, en nabo s til v og den mindste kant fra v (i dette tilfælde den til s). | |
|
Når vi skal arbejde videre har vi to muligheder: Vi kan bygge ud fra v eller s. Ud fra samme argument som ovenfor, vælger vi den mindste kant fra v eller s til deres naboer. Dette fortsætter vi med indtil alle knuder V er i vores løsning. | ||
| Prioritetskø til kanterne |
Dette lader sig bedst implementere med en prioritetskø, hvor kanterne prioriteres efter længde, og prioriteres kortest længde først. Vi lader kun de kanter, der fører fra knuder i vores delløsning til naboer uden for delløsningen, være i prioritetskøen. Efterhånden som knuder føjes til, føjes der også nye kanter til prioritetskøen. | |
|
Lad os konkretisere algoritmen: | ||
| Pseudo 5: Prioritet-først søgning |
| |
|
Prioritetskøen implementeres naturligvis med en heap, hvorfor alle operationer på prioritetskøen tager O(log |E|). Da hver kant i E på et tidspunkt indsættes i prioritetskøen og hver knude i V giver anledning til, at der udtages en kant, bliver den samlede tidskompleksitet O(|V| |E| log |E|). | ||
|
Algoritmen kom først frem i 1957 [Prim57]. Prim brugte dog ikke en heap, men et array til at implementere prioritetskøen. Prims algoritme fik derfor en ringere tidskompleksitet på O(|V|3). | ||
|
4.2 Kruskals algoritme | ||
|
En ganske anden algoritme er Kruskals algoritme ([AHU75] s.173-76). | ||
| Ikke lave cycler |
Kruskals idé er at fjerne alle kanter fra grafen og smide dem ind i en prioritetskø. Dernæst tager man kanter ud fra prioritetskøen, og sætter dem tilbage i grafen, men hvis en kants indsættelse vil betyde, at der opstår en cycle, smider man den i stedet væk. Da grafen før var sammenhængende fører dette naturligvis til et udspændende træ, og man kan bevise, at det samtidig vil være et minimalt udspændende træ. | |
| Union-Find |
Det vanskelige i Kruskals algoritme er at besvare spørgsmålet: "Hvis jeg tilføjer kanten e, bliver der så en cycle?" Hvis e forbinder u og v kan vi i stedet stille et andet spørgsmål: "er u og v allerede forbundet?". Man kan besvare dette spørgsmål vha. en Union-Find algoritme [Sedgewick92] s. 441-49. | |
|
Tidskompleksiteten for Kruskals algoritme er O(|E| log |E|). | ||
|
5. Dybde-først søgning | ||
| Find ud af labyrint |
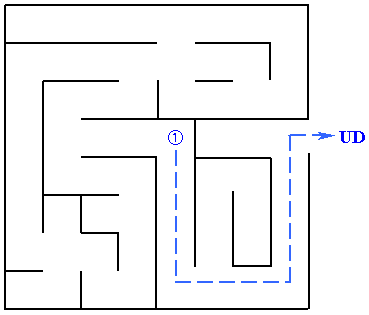
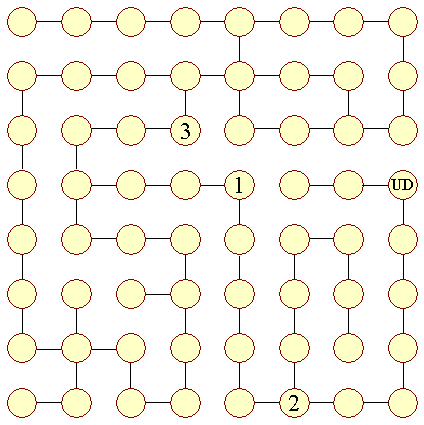
Der findes sagn og eventyr om mennesker, der er blevet holdt fangen i store labyrinter, som de ikke har kunnet finde ud af. Situationen kunne f.eks. være, at en person var placeret ved (1) i følgende labyrint: | |
| Figur 12: Labyrint |
| |
| Mangler overblik |
Den stiplede linie viser den korteste vej ud af labyrinten. Nu er det største problem for en person, der skal finde ud, at han ikke kan få det overblik vi har. Han kan ikke se over væggene. Det betyder at han ikke kender den korteste vej når han begynder at gå i sin søgen efter udgangen. Når vi derfor skal give ham en metode til at finde ud, må vi være forberedt på, at han ofte vil komme til at gå længere. | |
|
Metoden er meget enkel, og er kendt siden det 19. årh. [Lucas82], og henregnes i almindelighed til Trémaux. Først vil vi dog omforme labyrinten. | ||
| Inddele labyrint i felter |
Ved at inddele vores labyrint i felter og repræsentere hvert felt med en knude, kan vi omforme problemet så det bliver i termer af en graf. Hvis to felter er naboer, dvs. de ikke er adskilt af en mur, skal de også være naboer i grafen. | |
|
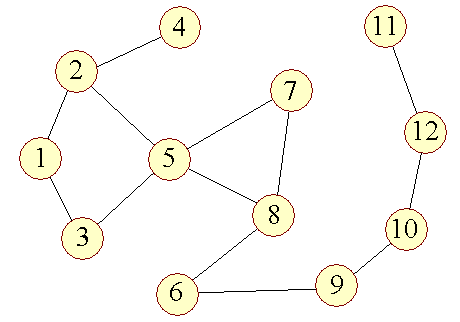
Vores labyrint kan på denne måde repræsenteres ved følgende graf: | ||
| Figur 13: Labyrint som graf |
| |
|
Problemet er nu omformet til at skulle finde en sti, evt. den korteste, mellem de to knuder (1) og UD. | ||
|
Problemet er blot, at de teknikker vi har til at løse dette problem kræver, at vi kender hele grafen. | ||
|
Det er netop problemet! Hvis vi havde et kort over labyrinten, så sad vi ikke i labyrinten og læste grafteori, men var allerede på vej ud! | ||
| En labyrint er ét rum |
Vi må altså gå på opdagelse! Det værste problem vi har, er når vi møder skilleveje. Hvilken skal vi vælge? Man kan få en idé til svaret på dette, ved at se abstrakt på labyrinten. En gang har vægge, et rum har vægge! Når vi står i et labyrint, befinder vi os derfor i et rum; hvor væggene er lidt længere end normalt. Hvis man stod i et normalt rum ville man kunne se døren for sig, og det ville ikke være noget problem at finde ud. Så vi slukker lyset. | |
| Følge væggen rundt |
Længden af vores arme svarer til det begrænsede overblik man har i en labyrint. Vi må nu føle os frem, og den oplagte løsning er at famle sig vej ud til væggen og følge den rundt, indtil vi møder døren. | |
|
Vi bruger nu samme teknik på labyrinten. Vi går langs med den ene væg. Mht. skilleveje betyder det, at vi må beslutte os for altid at gå til den samme side (højre eller venstre). | ||
|
Hvis vi prøver teknikken på vores labyrint, kan vi vælge altid at gå til venstre. Vi starter med at gå nedad og ved knude (2) går vi til venstre. I bunden af blindgyden vender vi og går tilbage og kommer nu igen til (2), hvor vi igen går til venstre og op mod UD. | ||
|
Nu kunne man måske få betænkeligheder. Hvad med cycler? Man kan hurtigt se om, og evt. hvornår, det kan være et problem ved igen at simplificere labyrinten til et rum. Betragt følgende figur: | ||
| Figur 14: Cycle i labyrint |
| |
|
Den store søjle i midten gør, at grafversionen vil være domineret af en cycle. Nu er det klart, at det hele står og falder med om vi famler os frem til søjlen, eller om vi finder ydervæggen. Hvis vi begynder at gå rundt om søjlen, bliver vi aldrig færdige, men finder vi ydervæggen er der igen problemer. | ||
|
"Gå rundt om søjle"-problemet er kun et problem; hvis vi aldrig opdager det. Hvis vi opdager det, kan vi blot vælge at følge den modsatte væg i stedet. | ||
| Gå fra en søjle til en anden søjle |
Man kan stadig forestille sig en situation hvor dette går galt, nemlig den at der er to søjler i rummet, og vi på det tidspunkt vi vælger at gå til modsatte væg står mellem søjlerne. Der er derfor ingen vej uden om "kom en halv ton ris i lommen, og klip hul"-teknikken. I graf-repræsentationen vil det sige, at vi mærker kanter, så vi ikke to gange passerer fra en knude til en naboknude, af samme kant. Vi vil nemlig ikke forhindre, at vi går tilbage, men kun, at vi går i samme retning ad den samme kant to gange! | |
| Mærkning af passager |
I praksis kan vi lave en sådan mærkning ved at mærke enderne af kanterne, som vi vil kalde passager, med et af to mulige mærker: F, der angiver at vi kom ind i knuden ad denne passage første gang vi besøgte den (F: First), og E for enhver anden passager vi benytter (E: Exit). Når man først har mærket en passage kan mærket aldrig ændres, eller fjernes igen. | |
|
Denne teknik bruges i Trémaux' algoritme, hvor alle passager initielt er umærkede, og startknuden er s: | ||
| Pseudo 6: Trémaux' algoritme |
| |
| Besøger alle knuder i grafen |
I denne algoritme, der vil besøge alle knuder i grafen, kan man naturligvis blot indsætte en kontrol af om v er UD. Samtidig bemærker man, at der i Trémaux' algoritme ikke er noget med højre og venstre. Det er fordi der generelt ikke er noget, der hedder højre og venstre i en graf. Da vi mærker passager, er der heller ikke noget behov for konsekvens mht. højre og venstre, blot vi ikke går en vej vi allerede har prøvet! | |
|
Det er nyt at vi tænker i passager, så lad os tydeligøre det med et lille eksempel: | ||
| Figur 15: Trémaux' passage-idé |
| |
|
Vi befinder os i knuden s og vil nu gå hele grafen igennem, uden at gå i ring. Vi vil ikke længere søge en speciel knude UD, da det er trivielt at stoppe når vi finder den knude vi søger. Vi vil i stedet fokusere på, at vi besøger alle knuder, og dermed naturligvis også en evt. UD-knude. | ||
|
Vi starter i S og mærker passage (0) E i skridt 3. Ved ankomst til A mærker vi passage (1) F i skridt 4, da det er første gang vi kommer til knude A. Vi går nu tilbage til skridt 2, og i skridt 3 mærker vi passage (2) E på vej til knude B. Ved ankomst til knude B mærker vi passage (3) F, da det er første gang vi kommer til knude B. Vi forlader nu knude B gennem passage (4), som vi mærker E og ankommer til knude C, via passage (5), som vi mærker F, da det er første gang vi kommer til knude C. Vi tager dernæst til knude A, via passage (6), som vi mærker E, og ankommer gennem passage (7), som mærkes E, da det ikke er første gang vi besøger knude A. Da knude A havde mærkede passager går vi i samme skridt 4 tilbage til knude C. Knude C forlades via passage (8), som mærkes E, og vi ankommer til knude S gennem passage (9), som vi mærker E. Da knude S har mærkede passager går vi tilbage til C. Da C ikke har flere umærkede passager går vi tilbage til B via passagen mærket F i skridt 5. Dette gentager sig for knuderne B og A, og vi ankommer til knude S via skridt 5. I det næste skridt 5 (efter en tur om skridt 2) terminerer vi. | ||
|
Man kan vise, at Trémaux' algoritme vil passere alle kanter i grafen netop én gang i hver retning. Derfor er tidskompleksiteten O(|E|). | ||
|
Trémaux' algoritme kaldes Dybde-først søgning, og har en række umiddelbare resultater. | ||
|
Grafens knuder og de kanter, der har en passage med et mærke F, udgør et udspændende træ: dybde-først søgetræet. Man kan se dette ved, at alle knuder (undtagen S) får en passage med mærket F når vi går ind i dem første gang, og netop kun det ene mærke F. Vi lader kanter mærket med F være kanter til faderen i træet og S bliver derved roden i træet. | ||
|
Vi har tidligere set på bredde-først søgning (Moores algoritme). Dybde-først og bredde-først er to forskellige måder at løse samme problem på: At besøge alle knuder i en graf. | ||
| Slår lyn i grafen |
Dybde-først søgning vil strejfe langt omkring, mens bredde-først søgning vil udbygge sit område omkring startknuden, og vil generelt brede sig mere som ringe i vandet. I modsætning til dybde-først søgning, der slår lange lyn ud i grafen. | |
|
6. Repræsentation | ||
|
Der findes to udbredte metoder til at repræsentere grafer. | ||
|
6.1 Nabo-matrice | ||
| Simple grafer |
Den første kaldes en nabo-matrice (eng.: adjacency matrix). Den kan bruges til at repræsentere simple grafer. Simple grafer, er grafer, der ikke har parallelle kanter. En nabo-matrice N er en matrix af booleans. N[u][v] fortæller om der findes en kant mellem knuderne u og v. N[u][u] fortæller derfor om der er en løkke på knuden u. | |
|
For grafer vil nabo-matricen være symetrisk, da N[u][v] = N[v][u]. | ||
| Orienteret |
Lader man den første dimension i nabo-matricen være startknuden og den anden slutknuden, kan man repræsentere en orienteret graf. | |
| Tynd og tæt graf |
Nabo-matricer bruges sjældent i praksis. Det skyldes, at grafer i de fleste anvendelser er tynde. En tynd graf er en graf med relativ få kanter pr. knude, mens en tæt graf har relativ mange kanter pr. knude. Der kan i en graf være vilkårlig mange kanter, så det er underforstået at begreberne tynd og tæt knytter sig til simple grafer. | |
|
Ulempen ved at repræsentere tynde grafer i en nabo-matrice er pladsforbruget. Det er naturligvis kun et reelt problem ved grafer med mange knuder. | ||
|
6.2 Indfalds-liste | ||
|
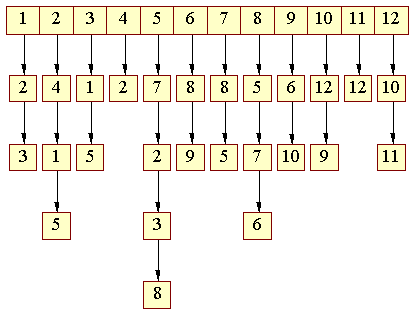
Man bruger i stedet en anden repræsentation, der kaldes en indfalds-liste (eng.: incidence list). En indfalds-liste er et array af lister. Betragt følgende indfaldsliste: | ||
| Figur 16: Indfalds-liste |
| |
|
Der repræsenterer følgende graf: | ||
| Figur 17: Grafen fra indfalds-listen |
| |
|
Som det ses, er hver kant repræsenteret to gange. Det er nødvendigt, da det ellers ville blive vanskeligt at bevæge sig rundt i grafen, hvis vi kun havde enkelt-repræsentation. Vi vil ikke fra en vilkårlig knude kunne se alle dens naboknuder ved at gennemløbe dens knudeliste. | ||
|
Når vi repræsenterer en orienteret graf bruger vi naturligvis ikke dobbelt-repræsentation, da man netop kun kan bevæge sig den ene vej ad en orienteret kant. | ||
|
Referencer | ||
| [AHU75] | A.V. Aho, J.E. Hopcroft og J.D. Ullman, "The Design and Analysis of Computer Algorithms", Addison-Wesley, 1975 | |
| [Dijkstra59] | E.W. Dijkstra, "A Note on Two Problems in Connection with Graphs", Numerische Math., Vol. 1, 1959, pp 269-271. | |
| [Floyd62] | R.W. Floyd, "Algorithm 97: Shortest Path", Comm. ACM, Vol. 5, 1962, p. 345. | |
| [Ford56] | L.R. Ford Jr., "Network Flow Theory", The Rand Corp., P-923, August, 1956. | |
| [Lucas82] | ? | |
| [Moore57] | E.F. Moore, "The Shortest Path Through a Maze", Proc. Internat. Symp. Switching Th., 1957, Part II, Harvard Univ. Press, 1959, pp. 285-292. | |
| [Prim57] | ? | |
| [Sedgewick92] | Robert Sedgewick, "Algorithms in C++", Addison-Wesley, 1992. | |
|
Repetitionsspørgsmål | ||
| 1 | Hvad er en løkke? | |
| 2 | Hvad er en isoleret knude? | |
| 3 | Hvad er parallelle kanter? | |
| 4 | Hvad er graden? | |
| 5 | Hvad er en sti? | |
| 6 | Hvad er længden af en sti? | |
| 7 | Hvad er en cycle? | |
| 8 | Hvad er en simpel sti? | |
| 9 | Hvad er en sammenhængende graf? | |
| 10 | Hvad er en orienteret graf? | |
| 11 | Hvad er en stærkt sammenhængende graf? | |
| 12 | Hvad er anti-parallelle kanter? | |
| 13 | Hvad er ind/ud-graden? | |
| 14 | I hvilken forstand er et træ en graf? | |
| 15 | Hvad er en skov? | |
| 16 | Hvad er en Euler-sti? | |
| 17 | Hvornår har en graf en Euler-sti? | |
| 18 | Moores, Dijkstras og Fords algoritmer mærker knuder. Hvad er det for knuder? | |
| 19 | Hvordan finder man den korteste sti ud fra mærkerne, når Moores, Dijkstras eller Fords algoritme terminerer? | |
| 20 | Hvordan undgår man at genveje i forbindelse med Moores algoritme? | |
| 21 | Hvad vil det sige at mærkerne i Moores algoritme spreder sig som "ringe i vandet"? | |
| 22 | Hvorfor vil det i snit tage dobbelt så lang tid at finde alle korteste stier, i Moores algoritme, end hvis vi stoppede med den søgte knude v? | |
| 23 | Hvilke grafer virker Moores algoritme ikke på, og hvorfor ikke? | |
| 24 | Hvorfor er O(|V|2) en dårligere tidskompleksitet end O(|E|)? | |
| 25 | Hvilke grafer virker Dijkstras algoritme ikke på, og hvorfor ikke? | |
| 26 | Hvorfor er O(|E||V|) en dårligere tidskompleksitet end O(|V|2)? | |
| 27 | Hvilke grafer virker Fords algoritme ikke på, og hvorfor ikke? | |
| 28 | Virker Fords algoritme for grafer med negative cycler? | |
| 29 | Hvad er et minimalt udspændende træ? | |
| 30 | Hvad er idéen i prioritet-først søgning? | |
| 31 | Hvad er idéen i Kruskals algoritme? | |
| 32 | Hvordan kan man altid finde ud af en labyrint uden cycler? | |
| 33 | Hvorfor er cycler i en labyrint et problem? | |
| 34 | Hvad kan man sammenligne en labyrint med? | |
| 35 | Hvordan kan man lave en graf ud fra en labyrint? | |
| 36 | Beskriv kort Trémaux' passage-idé. | |
| 37 | Hvilken algoritme kalder man også bredde-først søgning, og hvorfor? | |
| 38 | Hvilken algoritme kalder man også dybde-først søgning, og hvorfor? | |
| 39 | Hvad er en nabo-matrice? | |
| 40 | Hvad er en indfalds-liste? | |
|
Svar på repetitionsspørgsmål | ||
|
|