int tabel[] = new int[N];
Ikke aftagende orden

int count[] = new int[M];
Eksempel med counting sort
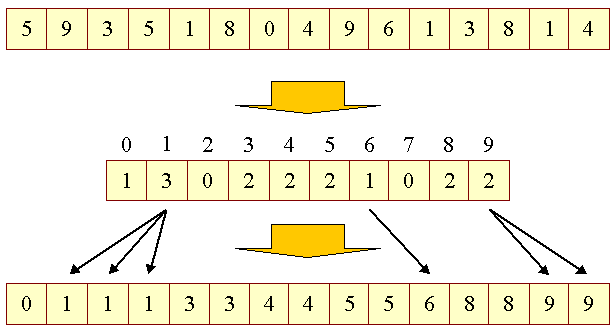
Counting sort
void countingSort(int[] tabel) {
int count[] = new int[M];
// 'count' initialiseres til 0 (ikke nødvendigt i Java/C#)
for (int i=0; i<count.length; i++)
count[i] = 0;
// der laves i 'count' en statistik over elementerne i 'tabel'
for (int i=0; i<tabel.length; i++)
count[tabel[i]]++;
// elementerne føres tilbage til det oprindelige array 'tabel'
int pos=0;
for (int i=0; i<count.length; i++)
while (count[i] > 0) {
tabel[pos] = i;
count[i]--;
pos++;
}
}
Sorterede delmængde udvider sig
 |
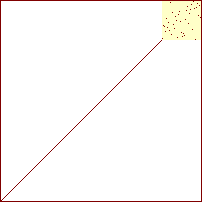
I det følgende skal vi se flere sorteringsalgoritmer der gradvist sorterer et array af integers. For at få et indtryk af hvordan sorteringen udvikler sig vil vi anvende nogle specielle diagrammer [Sedgewick92] (Sedgewick's bog indeholder mange gode diagrammer), som vi vil kalde sorterings-diagrammer. Diagrammerne viser en afbildning af et array, som giver et visuelt indtryk af hvor sorteret det er. Funktionen er ganske enkel:
| f(x) = array[x] |
Funktionen afbilder index over i elementet.
Hvis vi f.eks. har arrayet:
Permutation af [0:9]
 |
Vil det blive afbildet som:
Sorterings-diagram for arrayet
 |
Det giver naturligvis et indtryk af at tallene ikke er sorterede, men vigtigere er billedet når de er sorterede:
Sorterings-diagram for sorteret array
 |
Den matematisk mindede vil her bemærke identitets-funktionen. Grunden til at vi netop får identitets-funktionen, og dermed en lige linie, skal findes i de tal vi har valgt at sortere. Arrayet indeholder oprindelig en permutation af index-tallene. Når de sorteres opnår man netop identitets-funktionen.
Hvis man sorterer en permutation vil man kunne genkende en sorteret del af et arrayet som en linie med en vis hældning. Da vi arbejder med en permutation af index kan linien aldrig have en hældningskoefficient på mindre end én, men hvis der mangler tal i talrækken vil den være større end én.
Når vi i det følgende bruger disse illustrationer, vil vi anvende et array med 200 tal, da det giver en passende størrelse på diagrammet, når hvert tal repræsenteres med en pixel.
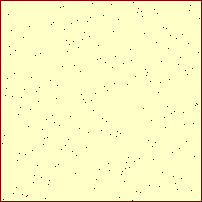
Sorterings-diagram for fuldstændig usorteret array med 200 tal
 |
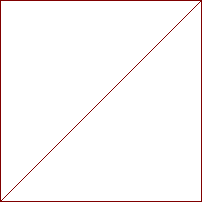
Sorterings-diagram for sorteret array med 200 tal
 |
Sorterings-diagram for delvist sorteret array med 200 tal
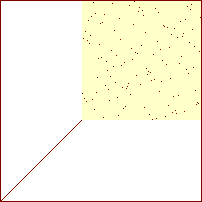 |
Realtids-diagram fra udvalgs-sortering
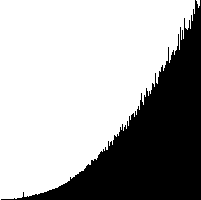 |
De fleste sorteringsalgoritmer har én operation til fælles. Det skyldes at flertallet af algoritmer arbejder på selve arrayet mens det sorteres, dvs. de flytter ikke elementer over i et andet array (som vi gjorde i Counting sort), men flytter rundt på dem i ét og samme array.
Det at flytte rundt i det samme array gøres ved ombytninger af to elementer. Denne operation bruges meget, hvorfor vi vil starte med at erklære den som metode, og anvende den i resten af kapitlet.
Metoden hedder swap og ombytter to elementer, angivet ved deres index.
Swap
void swap(int[] tabel, int x, int y) {
int temp = tabel[y];
tabel[y] = tabel[x];
tabel[x] = temp;
}
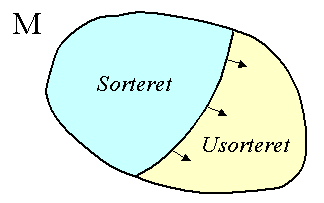
I udvalgssortering er den sorterede del, den forreste del af arrayet. Idéen i udvalgssortering er at finde det mindste element i den usorterede del af arrayet, og føje det til den sorterede del. I følgende figur er den sorterede del blå, og den endnu ikke sorterede del gullig. Den plads i arrayet, hvor det næste element, fra den usorterede del, der skal føjes til den sorterede del, skal placeres, er markeret med en stærkere gul farve.
Figur 11:
Delvist sorteret array
 |
Som det ses skal det nye element indsættes efter den sorterede del af arrayet. Det skyldes, at der for alle elementer key i den gullige del må gælder, at key>=tabel[i-1], ellers ville et sådant element allerede være udtaget som det daværende mindste, hvilket ikke er sket. Algoritmisk skal man altså finde elementet, og dernæst foretage et swap mellem det og det element der følger efter det sorterede delarray.
Figur 12:
Det usorterede array
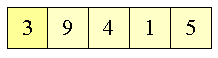 |
Figur 13:
swapper 3 og 1
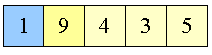 |
Figur 14:
swapper 9 og 3
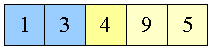 |
Figur 15:
4 swappes med sig selv
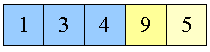 |
Figur 16:
Det sorterede array
 |
For hvert gennemløb udvides det sorterede delarray med netop ét element, hvorfor tidkompleksiteten for udvalgssortering er O(n2), implementationen bliver nemlig to for-løkker inden i hinanden:
selectionSort
void selectionSort(int[] tabel) {
for (int i=0; i<tabel.length-1; i++) {
int minIndex = i;
for (int candidatIndex=i+1; candidatIndex<tabel.length; candidatIndex++)
if (tabel[candidatIndex] < tabel[minIndex])
minIndex = candidatIndex;
swap(tabel, i, minIndex);
}
}
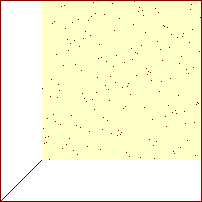
Sorterings-diagrammer for udvalgs-sortering
 |
 |
|
20 %
|
40 %
|
 |
 |
|
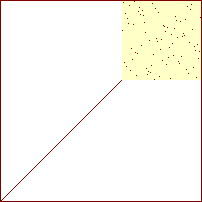
60 %
|
80 %
|
Realtids-diagram for udvalgs-sortering
 |
6. Indsættelsessortering
Indsættelses-sortering arbejder med den samme opdeling af arrayet som fremgår af figur 11. I indsættelsessortering udvider man også den sorterede del med ét element for hver iteration. I stedet for at gennemsøge den usorterede del efter det element, der skal placeres på position i, tager man det element der allerede står der, og indplacerer det i den sorterede del. Dette kræver at der gøres plads til elementet det sted hvor det skal placeres.
Gør plads til indsættelse af elementet fra position i
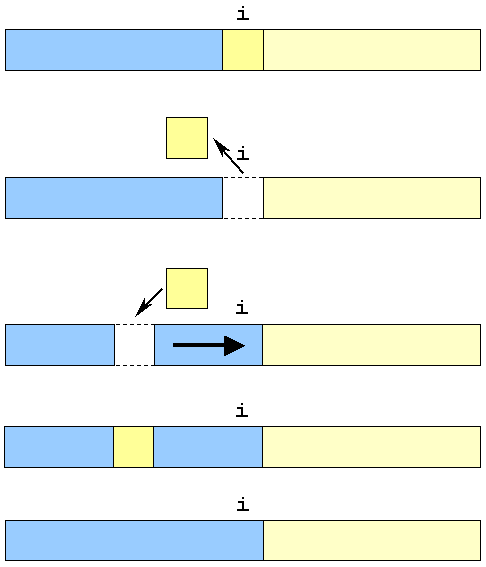 |
Denne plads skabes ved at flytte en del af de sorterede elementer én plads til højre. Dette er muligt, da vi netop fjernede elementet fra position i og dermed levner plads til at elementerne til venstre for position i kan flyttes én til højre.
Flytningen til højre kan kombineres med søgningen efter det sted hvor elementet skal indsættes ved at swappe det tilbage gennem de sorterede.
Lad os se et eksempel:
Første element er altid sorteret
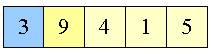 |
9 skal ikke flyttes
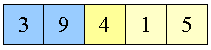 |
4 swappes på plads
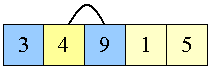 |
1 er den næste der skal på plads
1 skal swappes tre gange
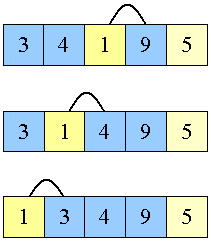 |
Dernæst skal 5 på plads
 |
5 swappes på plads
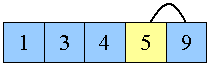 |
Det færdig-sorterede array
insertionSort
void insertionSort(int[] tabel) {
for (int i=1; i<tabel.length; i++) {
int runner = i;
while (runner>0 && tabel[runner-1]>tabel[runner]) {
swap(tabel, runner-1, runner);
runner--;
}
}
}
Sorterings-diagrammer for indsættelses-sortering
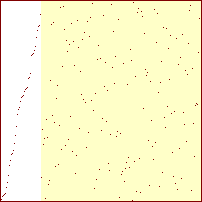 |
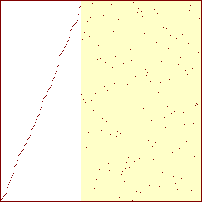 |
|
20 %
|
40 %
|
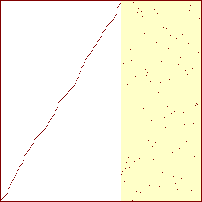 |
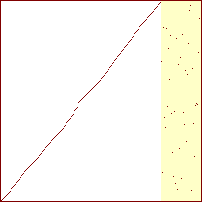 |
|
60 %
|
80 %
|
Realtids-diagram for indsættelses-sortering
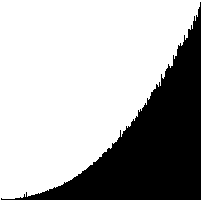 |
Boblesort bygger på idéerne fra udvalgssortering og indsættelsessortering.
Idéen er, at den sorterede del udbygges ved at det næste element sættes på plads på position i - altså idéen fra udvalgssortering, med at placere det rigtige element på positionen med det samme.
Det mindste element swappes ikke direkte på plads, men swappes tilbage gennem den usorterede del - altså idéen fra indsættelsessortering, med at vi rykker de andre så der bliver plads.
Måden hvorpå vi finder det mindste element i den usorterede del er derimod anderledes.
Vi lader os her inspirere af indsættelsessortering, men i stedet for at starte med at swappe fra det mindste element starter vi helt for enden af det usorterede del-array. Vi kommer derfor til at gøre et større arbejde, da vi starter swapningen helt ude for enden, men til gengæld slipper vi for at søge efter det mindste element. Når vi i løbet af vores swapning mod venstre, støder på det mindste element vil det vandre med os hele vejen tilbage til position i. De elementer vi har swappet inden vi nåede det mindste element er ikke spildt arbejde, da de alligevel skal bevæges i den retning de er blevet swappet.
Alt i alt lyder det som en udemærket idé, dog mere kompliceret end udvalgs- og indsættelsessortering.
Navnet boblesort kommer af de mange swaps vi laver. De får det til at "se ud" som om de små elementer "bobler op" igennem arrayet til deres pladser.
Lad os se et eksempel
Skal placere det rigtige element først
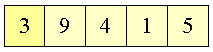 |
1 swappes tilbage gennem arrayet
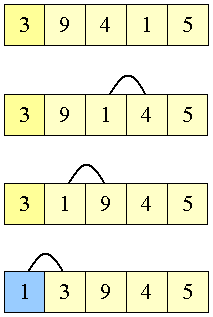 |
9 og 4 swappes
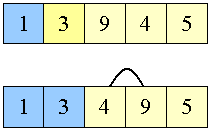 |
9 og 5 swappes
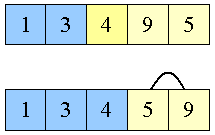 |
Det sorterede array
Sortering af array med 20 tal
10 26 11 28 12 16 23 13 17 25 21 15 18 24 14 19 22 29 20 27 10 11 26 12 28 13 16 23 14 17 25 21 15 18 24 19 20 22 29 27 10 11 12 26 13 28 14 16 23 15 17 25 21 18 19 24 20 22 27 29 10 11 12 13 26 14 28 15 16 23 17 18 25 21 19 20 24 22 27 29 10 11 12 13 14 26 15 28 16 17 23 18 19 25 21 20 22 24 27 29 10 11 12 13 14 15 26 16 28 17 18 23 19 20 25 21 22 24 27 29 10 11 12 13 14 15 16 26 17 28 18 19 23 20 21 25 22 24 27 29 10 11 12 13 14 15 16 17 26 18 28 19 20 23 21 22 25 24 27 29 10 11 12 13 14 15 16 17 18 26 19 28 20 21 23 22 24 25 27 29 10 11 12 13 14 15 16 17 18 19 26 20 28 21 22 23 24 25 27 29 10 11 12 13 14 15 16 17 18 19 20 26 21 28 22 23 24 25 27 29 10 11 12 13 14 15 16 17 18 19 20 21 26 22 28 23 24 25 27 29 10 11 12 13 14 15 16 17 18 19 20 21 22 26 23 28 24 25 27 29 10 11 12 13 14 15 16 17 18 19 20 21 22 23 26 24 28 25 27 29 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 26 25 28 27 29 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
bobleSort
void bobleSort(int[] tabel) {
for (int i=0; i<tabel.length; i++) {
int swaps = 0;
for (int p=tabel.length-1; i<p; p--)
if (tabel[p-1] > tabel[p]) {
swap(tabel, p-1, p);
swaps++;
}
// hvis vi ikke ændrede noget denne gang, kommer
// vi heller ikke til at gøre det næste gang => slut
if (swaps == 0)
break;
}
}
Sorterings-diagrammer for boblesort
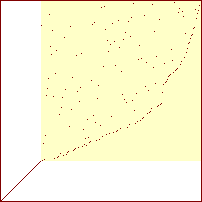 |
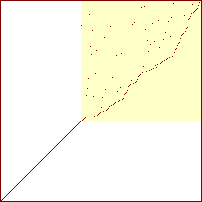 |
|
20 %
|
40 %
|
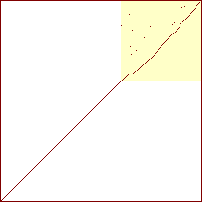 |
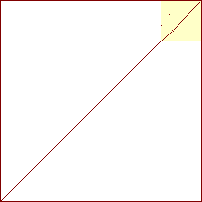 |
|
60 %
|
80 %
|
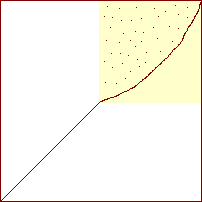
Generelt billede af et sorterings-diagram for boblesort
 |
Realtids-diagram for boblesort
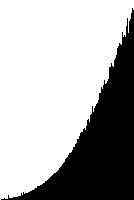 |
I modsætning til de tidligere algoritmers navne, fortæller navnet Quicksort [Hoare 62] ikke mere om den, end betegnelser som "Ultra Super de Luxe". Hvis man ser på tidskompleksiteten, i worst case, er den kun O(n2). Det der gør den attraktiv, er derimod den gennemsnitlige tidskompleksitet på O(n log n), og at den i praksis ofte er hurtigere end andre O(n log n) algoritmer Et andet træk ved den er, at den i forhold til algoritmer med worst case O(n log n) er uhyre simpel.
Lad os se den grundlæggende struktur i algoritmen:
bobleSort med kald af partition
void quickSort(int[] tabel, int left, int right) {
if (left < right) {
int midt = partition(tabel, left, right);
quicksort(tabel, left, midt-1);
quicksort(tabel, midt+1, right);
}
}
De tre parametre der gives til quickSort angiver en del af et array:
Figur 38:
Angivelse af delarray
 |
Stykket der indikeres ved left og right er med hele det gullige (og den blå), altså begge inklusiv.
quickSort sortere elementerne i det gullige område. Den gør det ved her at finde et element, der ved sin placering deler det hele i to. Dette element deler de andre på en sådan måde, at elemeneterne til venstre for det, er mindre end eller lig det, og alle elementer til højre for det, er større end eller lig det. De ville dermed være en anelse sorterede!
Nu er sandsynligheden for, at der findes et sådant element i den gullige usorterede del ikke stor. Man er derfor nød til at ændre på rækkefølgen af elementerne så det bliver tilfældet. Det er det, der er partitions opgave.
partition løser den ved ganske enkelt at fastslå at elementet længst til højre, tabel[right], skal være dette dele-element. Nu kan man naturligvis ikke regne med at alle andre elementer skulle være mindre end tabel[right], men så må man flytte tabel[right], på et tidspunkt. Efter at have registreret værdien af tabel[right] begynder delalgoritmen at flytte rundt på de andre elementer. Det gøres ved at arbejde med to index l og r, der starter i hver deres ende af det usorterede område. De arbejder sig nu ind mod "midten", hvor det er vores hensigt at placere tabel[right] til slut. For at det skal komme til at passe til sidst bliver tabel[l] og tabel[r] sammenlignet for hver gang en af dem rykkes, og hvis de begge er placeret forkert, dvs. tabel[l]>tabel[r] laves der et swap, hvorefter de er placeret rigtigt ifht. "midten". Hvis kun den ene er placeret forkert, flyttes den anden. Når de til slut krydser hinanden, laves der et swap mellem tabel[right] og det sidste element der var større end tabel[right], nemlig "midten". Herefter har partition løst sin opgave.
Lad os se et eksempel, der illustrerer teknikken. I figurene er det udvalgte "midt"-element blåt, fordi det i løbet af eksemplet ende med at være på plads. De endnu ikke sorterede elementer er gullige, og dem vi i denne omgang er færdige med at bearbejde er med en stærkere gul farve.
Bemærk at vi vælger det sidste element i delarrayet som vores "midt"-element, men venter med at placere det, da vi ikke ved hvor det skal være. En ting ved vi dog: Værdien af "midt"-elementet er 5; hvilket vi sammenligner de andre med.
Figur 39:
Swap af 9 og 4 over midten
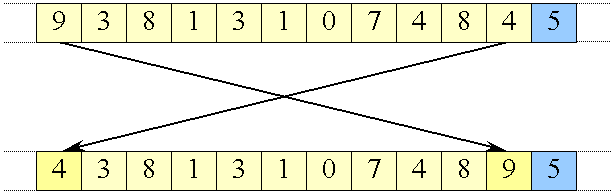 |
Her swapper vi 9 og 4 hen over midten, da 4 er mindre end 5 og 9 er større end 5. 5 skal senere placeres et eller andet sted mellem 9 og 4, og med den rækkefølge de har nu bryder de ordningen i forhold til 5. Derfor skal de swappes.
Efter de er swappet kan 5 placeres et sted mellem dem og de tre elementer vi isoleret set var sorterede i forhold til hinanden.
Swap af 8 og 4 over midten
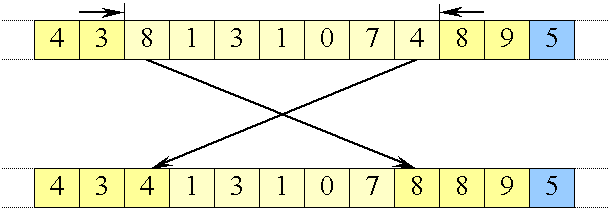 |
Swap af 7 og 5 placerer 5 i midten
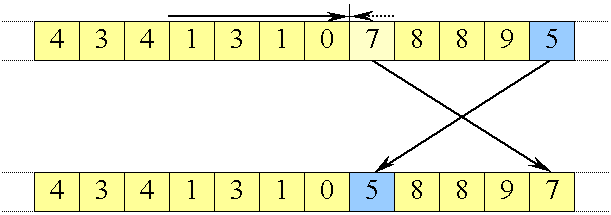 |
Som det ses af de to efterfølgende kald af quickSort, er quickSort rekursiv. Den generelle idé med rekursion, er at løse en (lille) del af et problem, og sende resten videre; hvor resten vel at mærke er samme slags problem som det oprindelige. Hvad er den løste del efter partition? Eftersom alle elementer til venstre for tabel[l] er mindre end eller lig den, og analogt større til højre for, er tabel[l] placeret rigtig, og skal aldrig flyttes igen! Det er måske overraskende, at den del af problemet quickSort vælger at løse hedder: "Placer et mere eller mindre tilfældigt element på sin endelige plads". Samtidig med at dette lille delproblem løses, ser man at resten herefter er tættere på at være løst, idet højre og venstre delarray er sorteret i forhold til hinanden. Rekursionen i quickSort løser dermed ikke ét lille delproblem, men snarere "1½".
Ved de efterfølgende kald af quickSort sorterer man naturligvis de to resterende delarrays. Da partition ikke fylder mere end nogle få linier vælger man ikke at lave den til et metodekald, men skriver den direkte ind i quickSort. Vores endelige algoritme bliver dermed:
quickSort
void quickSort(int[] tabel, int left, int right) {
if (left < right) {
int midValue = tabel[right];
int l = left;
int r = right-1;
while (l<=r) {
while (l<=r && midValue<=tabel[r])
r--;
while (l<=r && tabel[l]<midValue)
l++;
if (l<r) {
swap(tabel, l, r);
r--;
l++;
}
}
swap(tabel, l, right);
quickSort(tabel, left, l-1);
quickSort(tabel, l+1, right);
}
}
void quickSort(int[] tabel) {
quickSort(tabel, 0, tabel.length-1);
}
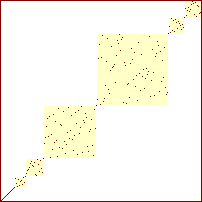
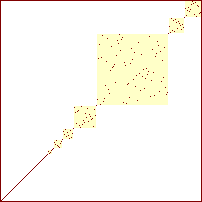
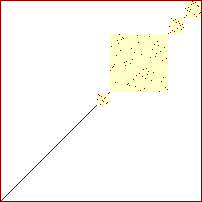
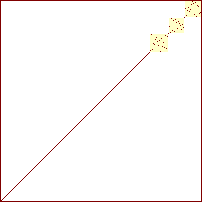
sorterings-diagrammer for quicksort
 |
 |
|
10 %
|
25 %
|
 |
 |
|
50 %
|
75 %
|
Procenterne angiver hvor stor en del af det samlede antal rekursive kald der er foretaget.
Man ser at arrayet hele tiden består af en række usorterede delarrays (kvadraterne), med mellemliggende elementer der er på plads (de punkter hvor kvadraterne mødes). Da kvadraterne ikke er sammenfaldende, hvis de projeceres ind på anden-aksen, ser man ligeldes den delvise sortering hvor elementerne i hvert delarray er placeret i det rigtige index-interval, men ikke på den rette position i det.
Lad os se et realtids-diagram fra en række testkørsler:
Realtids-diagram for quicksort
 |
Yderst til højre sorteres der 200.000 tal på 0.33 sekunder. Det er 20 gange så mange tal som boblesort på en tiendedel af den tid, den er om at sortere 10.000 tal.
Det viser at man vinder meget ved at vælge en O(n log n), selv om de er mere komplicerede end O(n2) algoritmerne.
9. Mergesort
Mergesort, eller flette-sortering, bygger på en grundlæggende teknik, der hedder fletning.
9.1 Fletning
Vi vil se på fletning af arrays eller delarrays. Lad os se et eksempel på to arrays der flettes over i et andet array.
De to arrays:
De to arrays der skal flettes
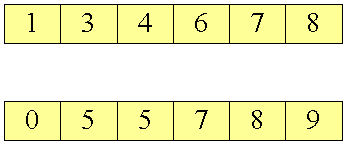 |
Det resulterende flettede array:
Det flettede array
 |
Man observerer at de to arrays som udgangspunkt var sorterede, og at det flettede array ligeledes er sorteret. Ordet fletning kommer bedst til sin ret hvis vi tegner resultatet med to "tråde", der går gennem elementerne, efter hvilket array de kom fra.
Fletningens sammenhæng
 |
Algortimisk er en fletning, et gennemløb af de to arrays. Man ser hele tiden på det "forreste" element i de to arrays, og en sammenligning er afgørende for, hvilken der skal over i resultat-arrayet. Man bliver ved på denne måde indtil begge arrays er "tømt" for elementer.
Den version af fletning vi skal bruge, arbejder ud fraat de to arrays, der skal flettes, ligger i forlængelse af hinanden i et større array. Resultatet skal placeres oven i de positioner de to arrays pt. ligger i.
Det er meget kompliceret at foretage fletningen uden et hjælpe-array. Vi vil derfor bruge et sådant. Vi vil kopiere de to delarrays over i et hjælpearray af samme længde som det store array de kommer fra, på de samme positioner, og dernæst flette fra det, tilbage i det gamle (Det kan måske undre, at vi er villige til at allokere et hjælpearray, der kan være betydelig større end nødvendigt, eftersom et hjælpearray med samme længde som de to delarrays tilsammen er tilstrækkeligt. Vi skal senere se hvorfor det er en god idé).
Fletning til mergesort
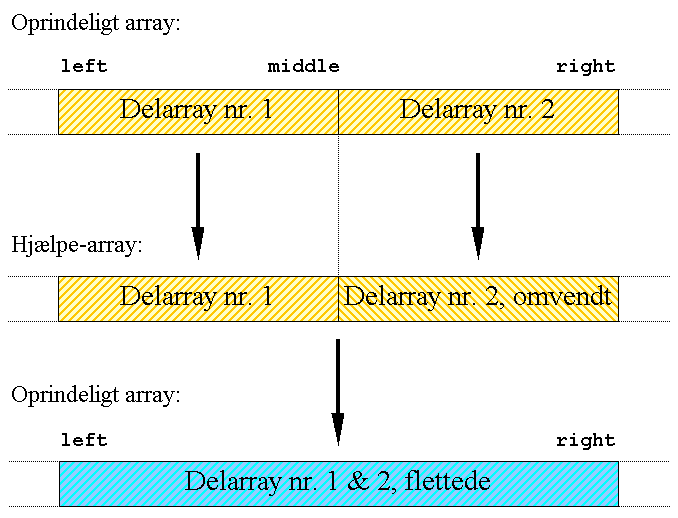 |
Vi vil i vores algoritme bruge left, som index for elementet længst til venstre i delarray nr. 1, og right, som index for elementet længst til højre i delarray nr. 2. Endelig vil vi bruge middle til at betegne index for elementet længst til højre i delarray nr. 1, og dermed skellet mellem delarray nr 1 og 2.
Hvorfor skal delarray nr. 2 vendes om? Idéen er at løse et problem, der opstår når det ene delarray er løbet tomt, mens der stadig er flere i det andet; uden at skulle lave speciel kode til situationen. Når vi vender det andet delarrays om, vender de største værdier ind mod hinanden. Når det ene løber tomt, kommer dets index til at pege på det største element i det andet delarray, og den vil derfor ikke flytte sig mere. Samtidig betyder det, at det andet delarray tømmes ved sammenligning med dette største element.
Vi skal derfor kopiere delarray nr. 2 over omvendt og sætte vores hjælpe-index r i dette delarray til right.
Del-arrays af tabel
 |
Del-array kopieret over i help
 |
Det første element flyttet fra help til tabel
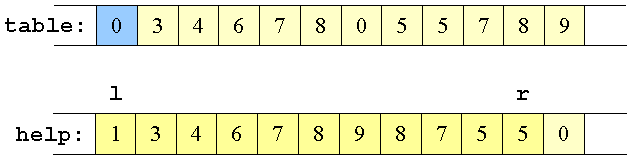 |
Med to elementer tilbage
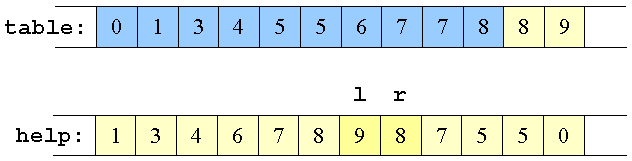 |
l og r på samme element
 |
Fletning
int l, r;
for (l=left; l<=middle; l++)
help[l] = tabel[l];
for (r=middle+1; r<=right; r++)
help[right - (r - middle) + 1] = tabel[r];
l = left;
r = right;
for (int res=left; res<=right; res++)
if (help[l] < help[r]) {
tabel[res] = help[l];
l++;
} else {
tabel[res] = help[r];
r--;
}
9.2 Sortering med fletning
Med ovenstående fletnings-algoritme kan man fra to sorterede del-arrays komme til et samlet sorteret del-array for dem begge. Vi kan bruge dette til at lave en rekursiv sortering, analog til quicksort. Idéen vil her være rekursivt at dele arrayet op i del-arrays ned til ét element og så flette tilbage, større og større delarrays, indtil hele arrayet er sorteret. Vi vælger derfor ved hvert rekursivt skridt at dele arrayet op i to lige store dele, kalde rekursivt for at få de to dele sorteret, og endelig selv flette de to delarrays. Vores endelige implementation bliver:
Sortering med fletning
int[] help = new int[tabel.length];
void mergeSort(int[] tabel, int left, int right) {
int l, r;
if (left < right) {
int middle = (left + right)/2;
mergeSort(tabel, left, middle);
mergeSort(tabel, middle+1, right);
for (l=left; l<=middle; l++)
help[l] = tabel[l];
for (r=middle+1; r<=right; r++)
help[right - (r - middle) + 1] = tabel[r];
l = left;
r = right;
for (int res=left; res<=right; res++)
if (help[l] < help[r]) {
tabel[res] = help[l];
l++;
} else {
tabel[res] = help[r];
r--;
}
}
}
void mergeSort(int[] tabel) {
mergeSort(tabel, 0, tabel.length-1);
}
Sorterings-diagrammer for mergesort
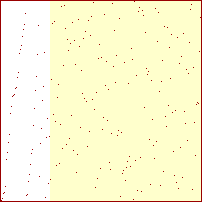 |
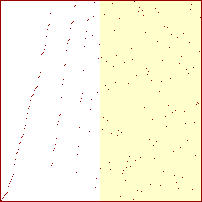 |
|
25 %
|
50 %
|
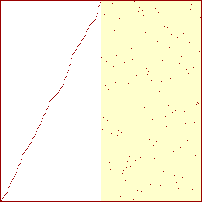 |
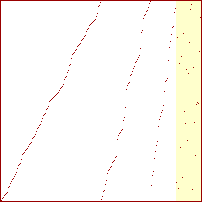 |
|
51 %
|
90 %
|
Procenterne er af det samlede antal rekursive kald. Springet mellem 50% og 51% er 5 kald.
Realtids-diagram for mergesort
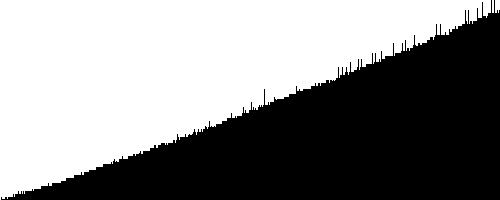 |
Mergesort har i worst case en tidskompleksistet på O(n log n), altså bedre end quicksort. Men som det ses har den ikke quicksorts enkelthed i koden, og er i praksis også langsommere.
I forbindelse med realtids-diagrammerne er der foretaget retouchering.
Det skyldes i første række, at alle diagrammerne har en lille forstyrrelse i starten af forløbet. Hvad den skyldes ved jeg ikke, men det kan evt. være JVM der holder en pause, hvor den ordner "et eller andet" - f.eks. initialiserer garbage collectoren.
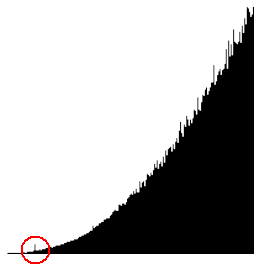 |
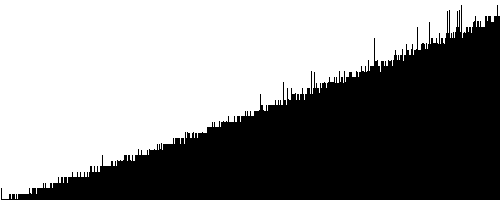 |